Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

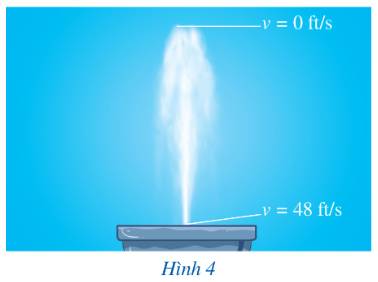
Khi xuất phát từ mặt đài phun nước, giọt nước có \(t = 0\).
Khi giọt nước đạt độ cao tối đa, \(v = 0\). Thay vào công thức tính tốc độ ta có:
\(\begin{array}{l}0 = 48 - 32t\\ - 48 = - 32t\\\,\,1,5 = t\end{array}\)
Vậy thời gian để giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là:
\(1,5 - 0 = 1,5\) (s).

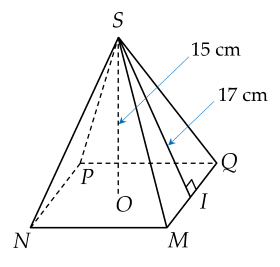
\(V_{S.MNPQ}=\dfrac{1}{3}.S_{MNPQ}.SO\)
\(\Rightarrow S_{MNPQ}=\dfrac{3.V_{S.MNPQ}}{SO}=\dfrac{3.1280}{15}=256cm^2\)
Xét tg vuông SOI
\(OI=\sqrt{SI^2-SO^2}\) (Pitago)
\(\Rightarrow OI=\sqrt{17^2-15^2}=8cm\)
Ta có
\(OI=\dfrac{MN}{2}\Rightarrow MN=2.OI=2.8=16cm\)
Ta có:
\(V=\dfrac{1}{3}.S_{MNPQ}.15=1280\left(cm^3\right)\)
\(\Rightarrow S_{MNPQ}=\dfrac{1280.3}{15}=256\left(cm^2\right)\)
\(\Rightarrow MN=\sqrt{256}=16\left(cm\right)\)

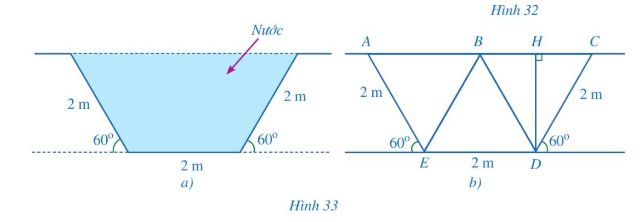
a, Do ACDE là hình thang cân nên
AC//DE suy ra AB//ED \( \Rightarrow {{\widehat B} _1} = {{\widehat E} _3},{{\widehat A} _1} = {{\widehat E} _1} = {60^0};{{\widehat C} _1} = {{\widehat D} _1} = {60^0}\)
Mà: AE//BD \( \Rightarrow {{\widehat B} _2} = {{\widehat E} _2}\)
Xét \(\Delta ABE\) và \(\Delta B{\rm{D}}E\) có: \({{\widehat B} _1} = {{\widehat E} _3}\) ; BE chung
\(\begin{array}{l}{{{\widehat B} }_2} = {{{\widehat E} }_2} \Rightarrow \Delta ABE = \Delta B{\rm{D}}E \Rightarrow A{\rm{E}} = B{\rm{D}} = 2m.\\AB = E{\rm{D}} = 2m\end{array}\)
Xét \(\Delta BC{\rm{D}}\) có \({{\widehat C} _1} = {60^0};B{\rm{D}} = C{\rm{D}} = 2m \Rightarrow \Delta BC{\rm{D}}\) đều.
Xét \(\Delta A{\rm{E}}B\) có \({{\widehat A} _1} = {60^0};AB = A{\rm{E}} = 2m \Rightarrow \Delta A{\rm{E}}B\) đều.
Vì: \(\Delta A{\rm{E}}B\) đều suy ra: BE = 2 m.
Xét \(\Delta BE{\rm{D}}\) có BD = BE = ED = 2m \( \Rightarrow \Delta BE{\rm{D}}\) đều.
b, Vì \(\Delta ABE,\Delta BC{\rm{D}}\) là các tam giác đều nên AB = BC = 2m.
Suy ra AC = AB + BC = 4m.
Do \(\Delta B{\rm{D}}C\) đều nên H là trung điểm của BC.
Suy ra HC = HB =\(\dfrac{{BC}}{2} = 1\)
Xét \(\Delta DHC\) vuông tại H ta có:
\(D{C^2} = D{H^2} + H{C^2}\) (theo định lý pythagore)
\(\begin{array}{l} \Rightarrow D{H^2} = D{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow DH = \sqrt 3 \end{array}\)
c, Diện tích hình thang cân AEDC là:
\({S_{A{\rm{ED}}C}} = \dfrac{1}{2}DH.(AC + E{\rm{D}}) = \dfrac{1}{2}\sqrt 3 (2 + 4) = 3\sqrt 3 (c{m^2})\)
Vậy diện tích mặt cắt phần chứa nước: \(3\sqrt 3 c{m^2}\)

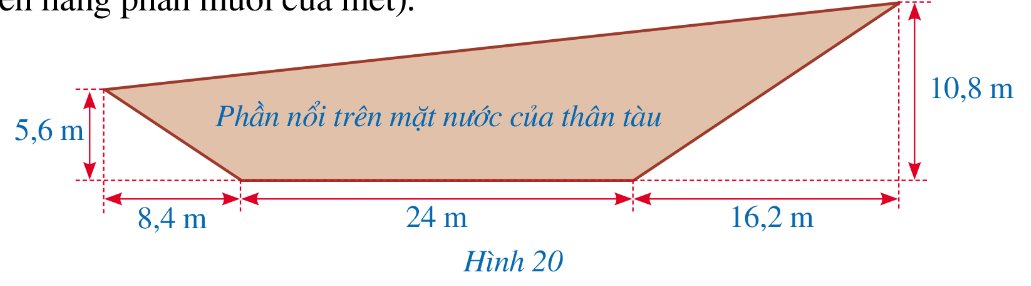
*) Áp dụng định lí Pythagore trong tam giác \(\Delta ABC\) vuông tại A có
\(A{C^2} = A{B^2} + B{C^2} = 5,{6^2} + 8,{4^2} = 101,92 \Rightarrow AC = \sqrt {101,92} \)
\(\Delta DEF\) vuông tại F có
\(D{F^2} = D{E^2} + E{F^2} = 16,{2^2} + 10,{8^2} = 379,08 \Rightarrow DF = \sqrt {379,08} \)
Kẻ \(AG \bot FG\)
Khi đó: \(FG = FE - GE = FE - AB = 10,8 - 5,6 = 5,2\)
Áp dụng định lí Pythagore trong \(\Delta AGF\) vuông tại G có
\(A{F^2} = A{G^2} + F{G^2} = 48,{6^2} + 5,{2^2} = 2389 \Rightarrow AF = \sqrt {2389} \)
Chu vi tứ giác ACDF là:
\(AC + CD + DF + AF = \sqrt {101,92} + \sqrt {379,08} + 24 + \sqrt {2389} \approx 102,4\)
Vậy chu vi của mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thủy là khoảng 102,4m.

\(C=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^{16}-1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^{32}-1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=x^{64}-1-x^{64}\)
\(C=-1\)
Vậy gtri của C không phụ thuộc vào x

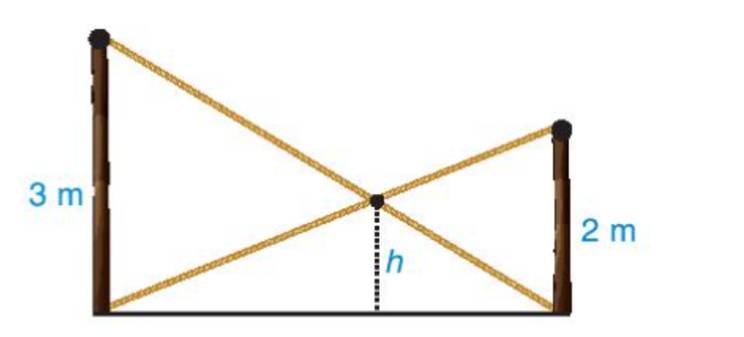
- Có AB // CD
=> \(\widehat {BAC} = \widehat {DCA}\) (2 góc so le trong)
\(\widehat {BDC} = \widehat {AB{\rm{D}}}\)(2 góc so le trong)
- Xét hai tam giác ABE và tam giác CDE, có \(\widehat {BAC} = \widehat {DCA};\widehat {B{\rm{D}}C} = \widehat {AB{\rm{D}}}\)
=> ΔABE ∽ ΔCDE
=> \(\frac{{C{\rm{D}}}}{{AB}} = \frac{{CE}}{{A{\rm{E}}}} = \frac{2}{3}\)
=> \(\frac{{CE}}{{A{\rm{E}}}} = \frac{2}{3}\)=> \(\frac{{CE}}{{CA}} = \frac{2}{5}\)
- Xét hai tam giác CEF và tam giác CAB có EF // AB
=> ΔCEF ∽ ΔCAB (theo định lý)
=> \(\frac{{F{\rm{E}}}}{{AB}} = \frac{{CE}}{{CA}} = \frac{2}{5}\)
=> \(\frac{{F{\rm{E}}}}{{AB}} = \frac{2}{5}\) => \(\frac{{F{\rm{E}}}}{3} = \frac{2}{5}\)=> \(F{\rm{E}} = 3.\frac{2}{5} = 1,2(m)\)
Vậy độ cao h là 1,2 m

Bài 10:
gọi vận tốc thực của tàu khi nước yên lặng là x km/h (x>o)
vận tốc của thuyền lúc đi là x-4 km/h
vận tốc của thuyền lúc về là x+4 km/h
thời gian thuyền di đến bến bên kia la 80/(x-4) h
thời gian thuyền di được khi quay về la 80/(x+4) h
vì thời gian cả di lẩn về là 8h20' (hay 25/3 h) nên ta có pt:
80/(x+4) + 80/(x-4) = 25/3
<=> 240x-960+240x+960=25x^2-400
<=> 25x^2-480x-400=0
dental' = (-240)^2 +25*400= 67600 (>0) căn dental'= 240
vậy pt có hai nghiệm
x1= (240-260)/25=0.0.......(loại)
x2=(240+260)/25=20 (nhận)
vậy vận tốc của tàu khi nước yên lặng là 20 km/h
nguồn: Toán học Lớp 8
Bài 12
Gọi thời gian để người đi xe máy đuổi kịp người đi xe đạp là a giờ (a>0)
Thời gian người đi xe đạp xuất phát trước xe máy là : 8h40'-7h=1h40'=5/3h
=>Quãng đường người đi xe đạp đi trước người đi xe máy là : 10.5/3=50/3(km/h)
Vì vận tốc của người đi xe máy là 30km/h , vận tốc của người đi xe đạp là 10km/h => cứ 1 h người đi xe máy lại đến gần người đi xe đạp một khoảng là : 30-10=20km
=> Thời gian để người đi xe máy đuổi kịp người đi xe đạp là : a=50/3 : 20 =5/6h=50'
=> Thời gian lúc 2 người gặp nhau là : 8h40' + 50'=9h30'
Vậy hai người gặp nhau lúc 9h30'.
nguồn: Bài tập Toán học Lớp 8
Bài còn lại tham khảo ở đây: Bài tập Toán học Lớp 8







a) Số nhiệt của thành phố A là:
\(I=-45+2\cdot40+10\cdot100-0,2\cdot40\cdot100-0,007\cdot40^2-0,05\cdot100^2+0,001\cdot40^2\cdot100+0,009\cdot40\cdot100^2-0,000002\cdot40^2\cdot100^2\)
\(I=-3345,2\)
b) Số nhiệt của thành phố B là:
\(I=-45+2\cdot50+10\cdot90-0,007\cdot50^2-0,05\cdot90^2+0,001\cdot50^2\cdot90+0,009\cdot50\cdot90^2-0,00000\cdot50^2\cdot90^2\)
\(I=-3780\)
a) Số nhiệt của thành phố A là:
�=−45+2⋅40+10⋅100−0,2⋅40⋅100−0,007⋅402−0,05⋅1002+0,001⋅402⋅100+0,009⋅40⋅1002−0,000002⋅402⋅1002I=−45+2⋅40+10⋅100−0,2⋅40⋅100−0,007⋅402−0,05⋅1002+0,001⋅402⋅100+0,009⋅40⋅1002−0,000002⋅402⋅1002
�=−3345,2I=−3345,2
b) Số nhiệt của thành phố B là:
�=−45+2⋅50+10⋅90−0,007⋅502−0,05⋅902+0,001⋅502⋅90+0,009⋅50⋅902−0,00000⋅502⋅902I=−45+2⋅50+10⋅90−0,007⋅502−0,05⋅902+0,001⋅502⋅90+0,009⋅50⋅902−0,00000⋅502⋅902
�=−3780I=−3780