Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Số nhiệt của thành phố A là:
\(I=-45+2\cdot40+10\cdot100-0,2\cdot40\cdot100-0,007\cdot40^2-0,05\cdot100^2+0,001\cdot40^2\cdot100+0,009\cdot40\cdot100^2-0,000002\cdot40^2\cdot100^2\)
\(I=-3345,2\)
b) Số nhiệt của thành phố B là:
\(I=-45+2\cdot50+10\cdot90-0,007\cdot50^2-0,05\cdot90^2+0,001\cdot50^2\cdot90+0,009\cdot50\cdot90^2-0,00000\cdot50^2\cdot90^2\)
\(I=-3780\)
a) Số nhiệt của thành phố A là:
�=−45+2⋅40+10⋅100−0,2⋅40⋅100−0,007⋅402−0,05⋅1002+0,001⋅402⋅100+0,009⋅40⋅1002−0,000002⋅402⋅1002I=−45+2⋅40+10⋅100−0,2⋅40⋅100−0,007⋅402−0,05⋅1002+0,001⋅402⋅100+0,009⋅40⋅1002−0,000002⋅402⋅1002
�=−3345,2I=−3345,2
b) Số nhiệt của thành phố B là:
�=−45+2⋅50+10⋅90−0,007⋅502−0,05⋅902+0,001⋅502⋅90+0,009⋅50⋅902−0,00000⋅502⋅902I=−45+2⋅50+10⋅90−0,007⋅502−0,05⋅902+0,001⋅502⋅90+0,009⋅50⋅902−0,00000⋅502⋅902
�=−3780I=−3780

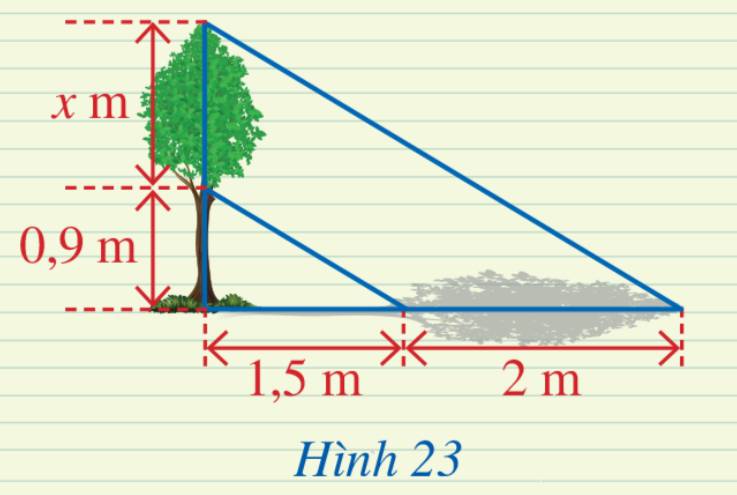
Đoạn thẳng AB biểu thị cho độ cao của cây, đoạn thẳng AD và DB biểu thị độ cao của thân và tán cây, đoạn thẳng AE và EC biểu thị độ dài cái bóng của thân cây và tán cây, đoạn thẳng DE và BC biểu thị cho các tia nắng.
Xét tam giác ABC với \(DE\parallel BC\) ta có:
\(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\) (Định lý Thales)
\(\begin{array}{l} \Rightarrow \frac{{0,9}}{x} = \frac{{1,5}}{2}\\ \Rightarrow 0,9.2 = 1,5x\\ \Rightarrow 1,8 = 1,5x\\ \Rightarrow x = 1,2\end{array}\)
Vậy độ cao \(x\) là 1,2 m.

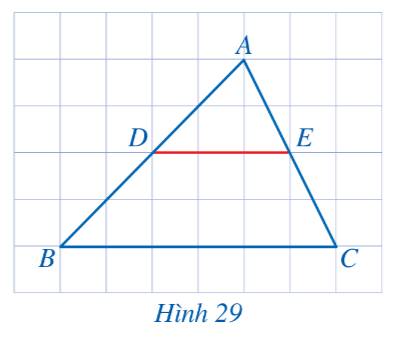
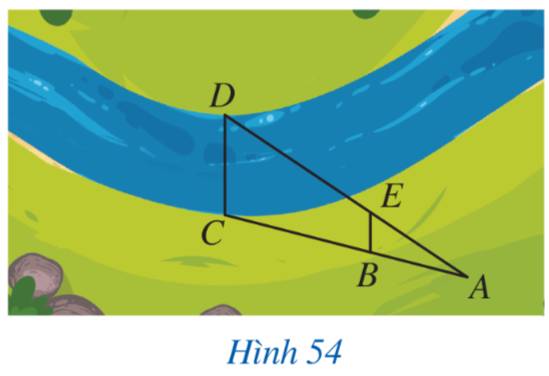
Quan sát hình ta thấy D và trung điểm của đoạn thẳng AB và E là trung điểm của đoạn thẳng AC.

Vì \(\Delta ABE \backsim \Delta ACD\) nên ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}} \Leftrightarrow \frac{{20}}{{50}} = \frac{8}{{CD}} \Rightarrow CD = 8.50:20 = 20\)
Vậy độ rộng của khúc sông là 20m.

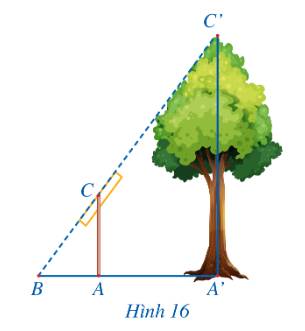
\(\left. \begin{array}{l}AC \bot A'B\\A'C' \bot A'B\end{array} \right\} \Rightarrow AC\parallel A'C'\)
Xét tam giác A’BC’ với \(AC\parallel A'C'\) có:
\(\frac{{AC}}{{A'C'}} = \frac{{BA}}{{BA'}}\) (Hệ quả của định lý Thales)
\( \Rightarrow \frac{{AC}}{{A'C'}} = \frac{{1,5}}{{4,5}} = \frac{1}{3} \Rightarrow A'C' = 3AC = 6m\)
Vậy cây cao 6m.

a) Quan sát hình 24, ta thấy:
Tung độ giao điểm của hai đường thẳng \({d_1},{d_2}\) đều bằng 2.
Nhận xét: Hai chuyển động đều có cùng tốc độ ban đầu là 2m/s.
b) Trong 2 đường thẳng \({d_1},{d_2}\) đường thẳng d2 có hệ số góc lớn hơn.
c) Từ giây thứ nhất trở đi, vật thứ hai có tốc độ lớn hơn vì đường thẳng d2 cao hơn đường thẳng d1 từ giây thứ nhất.

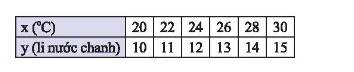
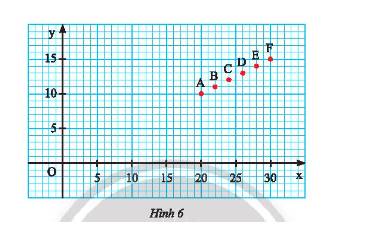
a) Điểm \(A\left( {20;10} \right);B\left( {22;11} \right);C\left( {24;12} \right);D\left( {26;13} \right);E\left( {28;14} \right);D\left( {30;15} \right)\)
Ta thấy mỗi cặp giá trị \(x;y\) tương ứng trong bảng là tọa độ của các điểm \(A;B;C;D;E;F\).

Nhìn vào biểu đồ, tương ứng với các mốc thời gian, số ở cột màu xanh biểu diễn GDP của Việt Nam và số ở cột màu đổ biểu diễn GDP của Singapore.
Ta xác định được GDP của hai nước trong các năm 2016, 2017, 2018 như sau:
Việt Nam:
Năm 2016: 205,3 tỉ đô la Mỹ
Năm 2017: 223,7 tỉ đô la Mỹ
Năm 2018: 245,2 tỉ đô la Mỹ
Singapore:
Năm 2016: 318,7 tỉ đô la Mỹ
Năm 2017: 341,9 tỉ đô la Mỹ
Năm 2018: 373,2 tỉ đô la Mỹ

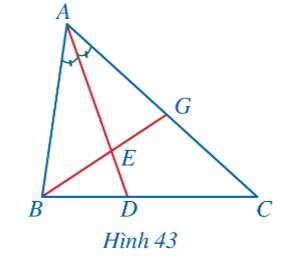
Xét tam giác ABC với đường phân giác AD ta có: \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) (Tính chất đường phân giác)
Xét tam giác ABG với đường phân giác AE ta có: \(\frac{{EB}}{{EG}} = \frac{{AB}}{{AG}}\)(Tính chất đường phân giác)
\( \Rightarrow \frac{{DB}}{{DC}}:\frac{{EB}}{{EG}} = \frac{{AB}}{{AC}}:\frac{{AB}}{{AG}} = \frac{{AG}}{{AC}}\) (đpcm)
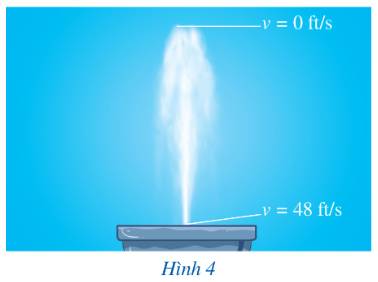


Khi xuất phát từ mặt đài phun nước, giọt nước có \(t = 0\).
Khi giọt nước đạt độ cao tối đa, \(v = 0\). Thay vào công thức tính tốc độ ta có:
\(\begin{array}{l}0 = 48 - 32t\\ - 48 = - 32t\\\,\,1,5 = t\end{array}\)
Vậy thời gian để giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là:
\(1,5 - 0 = 1,5\) (s).