Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

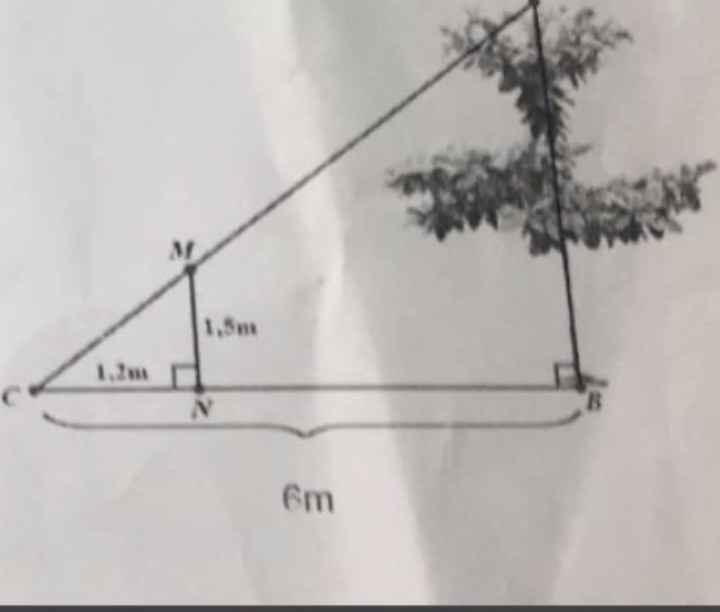
Ta có:MN\(\perp\)CB
AB\(\perp\)CB
Do đó: MN//AB
Xét ΔCAB có MN//AB
nên \(\dfrac{MN}{AB}=\dfrac{CN}{CB}\)
=>\(\dfrac{1.5}{AB}=\dfrac{1.2}{6}=\dfrac{1}{5}\)
=>AB=1,5*5=7,5(m)

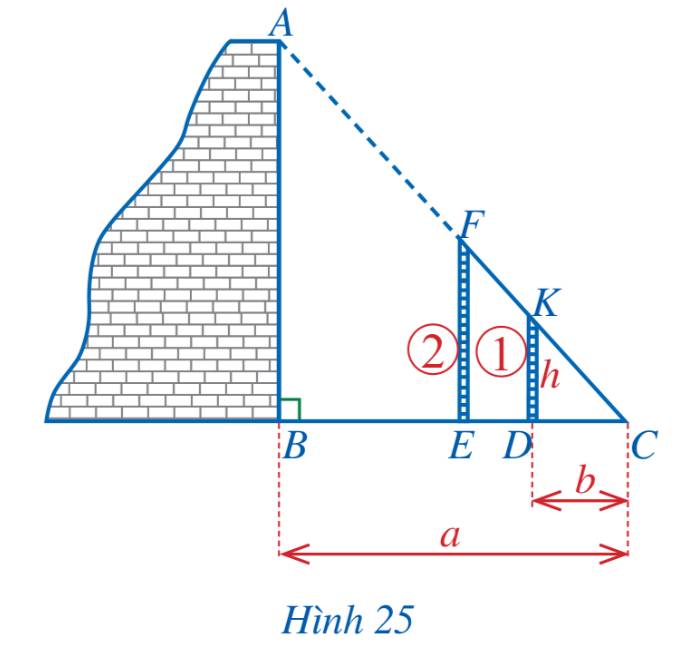
a) Cách tiến hành:
- Đặt hai cọc thẳng đứng, vuông góc với mặt đất sau đó di chuyển cọc 2 sao cho 3 điểm A, F, K thẳng hàng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất (3 điểm F, K, C thẳng hàng).
Sử dụng hệ quả của định lý Ta – let để tính chiều cao AB.
b) Ta có:
\(\left. \begin{array}{l}AB \bot BC\\DK \bot BC\end{array} \right\} \Rightarrow AB\parallel DK\)
Xét tam giác ABC với \(AB\parallel DK\) ta có:
\(\frac{{DK}}{{AB}} = \frac{{CD}}{{CB}}\) (Hệ quả của định lý Thales)
\( \Rightarrow AB = \frac{{DK.CB}}{{CD}} = \frac{{h.a}}{b}\).

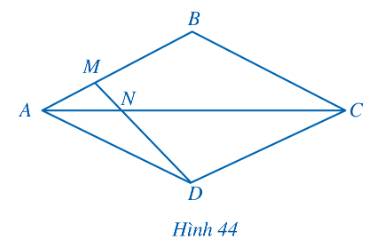
Gọi giao điểm hai đường chéo của hình thoi là O.
Khi đó AC vuông góc với BD tại O.
Vì ABCD là hình thoi nên \(AB = AD\) hay tam giác ABD cân tại A.
Khi đó AO vừa là đường cao, vừa là phân giác của tam giác ABD.
Xét tam giác AMD với AN là đường phân giác, ta có:
\(\frac{{ND}}{{NM}} = \frac{{AD}}{{AM}}\,\,\left( 1 \right)\) (Tính chất đường phân giác)
Mà \(AB = 3AM \Rightarrow \frac{{AB}}{{AM}} = 3 \Rightarrow \frac{{AD}}{{AM}} = 3\,\,\left( 2 \right)\)
Từ (1) và (2) ta có: \(\frac{{ND}}{{NM}} = 3 \Rightarrow ND = 3NM\).

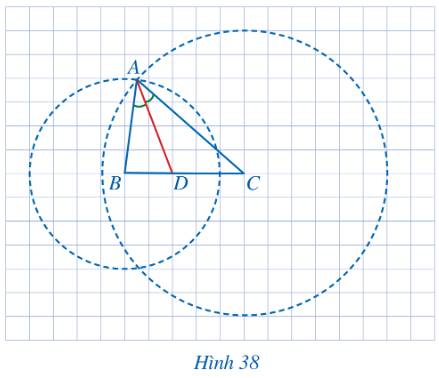
a) Ta thấy mỗi ô vuông có độ dài cạnh bằng 1cm.
Đoạn thẳng BD có độ dài bằng độ dài cạnh của 2 ô vuông nên BD dài 2 cm.
Đoạn thẳng DC có độ dài bằng độ dài cạnh của 3 ô vuông nên BD dài 3 cm.
b) Ta thấy AB là bán kính đường tròn tâm B. Mà bán kính đường tròn tâm B có độ dài 4 ô vuông, tương ứng với 4 cm nên AB dài 4 cm.
Ta thấy AC là bán kính đường tròn tâm C. Mà bán kính đường tròn tâm C có độ dài 6 ô vuông, tương ứng với 6 cm nên AB dài 6 cm.
c) Ta có: \(\frac{{DB}}{{DC}} = \frac{2}{3};\,\,\frac{{AB}}{{AC}} = \frac{4}{6} = \frac{2}{3}\)
Vậy \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\).

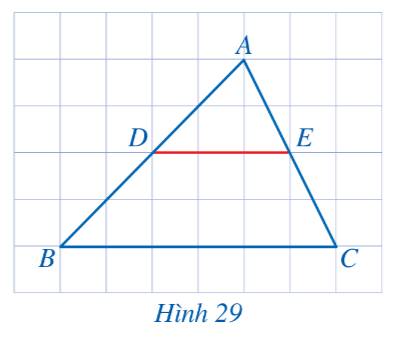
Quan sát hình ta thấy D và trung điểm của đoạn thẳng AB và E là trung điểm của đoạn thẳng AC.
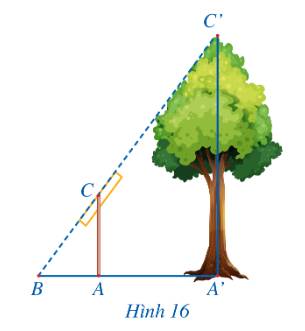

\(\left. \begin{array}{l}AC \bot A'B\\A'C' \bot A'B\end{array} \right\} \Rightarrow AC\parallel A'C'\)
Xét tam giác A’BC’ với \(AC\parallel A'C'\) có:
\(\frac{{AC}}{{A'C'}} = \frac{{BA}}{{BA'}}\) (Hệ quả của định lý Thales)
\( \Rightarrow \frac{{AC}}{{A'C'}} = \frac{{1,5}}{{4,5}} = \frac{1}{3} \Rightarrow A'C' = 3AC = 6m\)
Vậy cây cao 6m.