Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Số đo cung nhỏ AB=góc AOB( góc ở tâm)\(\Rightarrow\) Số đo cung nhỏ AB=60 độ
* Diện ích hình quạt tròn OAB là
\(S=\frac{\pi\times R2\times n}{360}=\frac{\pi\times9\times60}{360}=\frac{3}{2}\pi\approx\frac{3}{2}\times3,14\approx4,71\)cm2
* Số đo cung lớn AB= 360 độ - 60 độ =300 độ
Độ dài cung lớn AB là:
l=3,14*3*300/180=15,7 cm


Kiến thức áp dụng
+ Trên đường tròn đường kính R, độ dài cung n0 bằng :
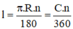

a) Vì TO là đường kính \(\Rightarrow\angle TMO=90\) mà \(M\in\left(O\right)\Rightarrow TM\) là tiếp tuyến của (O)
b) Xét \(\Delta TMC\) và \(\Delta TDM:\) Ta có: \(\left\{{}\begin{matrix}\angle MTDchung\\\angle TMC=\angle TDM\end{matrix}\right.\)
\(\Rightarrow\Delta TMD\sim\Delta TCM\left(g-g\right)\Rightarrow\dfrac{TC}{TM}=\dfrac{TM}{TD}\Rightarrow TC.TD=TM^2\)
c) Vì đường tròn đường kính TO có tâm I và đường tròn (O) cắt nhau tại M và N \(\Rightarrow\) IO là trung trực của MN \(\Rightarrow MN\bot TO\)
mà \(\Delta TMO\) vuông tại M \(\Rightarrow TM^2=TE.TO\) (hệ thức lượng)
mà \(TC.TD=TM^2\Rightarrow TC.TD=TE.TO\Rightarrow\dfrac{TC}{TE}=\dfrac{TO}{TD}\)
Xét \(\Delta TEC\) và \(\Delta TDO:\) Ta có: \(\left\{{}\begin{matrix}\angle OTDchung\\\dfrac{TC}{TE}=\dfrac{TO}{TD}\end{matrix}\right.\)
\(\Rightarrow\Delta TEC\sim\Delta TDO\left(c-g-c\right)\Rightarrow\angle TEC=\angle TDO\Rightarrow ODCE\) nội tiếp

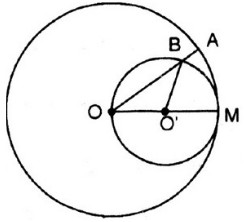
Đặt ˆMOB=αMOB^=α
⇒ˆMO′B=2α⇒MO′B^=2α (góc nội tiếp và góc ở tâm của đường tròn (O’))
Độ dài cung MB là:
lcungMB=π.O′M.2α1800=π.O′M.α900(1)lcungMB=π.O′M.2α1800=π.O′M.α900(1)
Độ dại cung MA là:
lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)
(Vì OM = 2O’M)
Từ (1) và (2) ⇒ sđcung MA = sđcung MB

Đặt ˆMOB=αMOB^=α
⇒ˆMO′B=2α⇒MO′B^=2α (góc nội tiếp và góc ở tâm của đường tròn (O’))
Độ dài cung MB là:
lcungMB=π.O′M.2α1800=π.O′M.α900(1)lcungMB=π.O′M.2α1800=π.O′M.α900(1)
Độ dại cung MA là:
lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)
(Vì OM = 2O’M)
Từ (1) và (2) ⇒ sđcung MA = sđcung MB

Xét ΔOBA vuông tại A có \(cosBOA=\dfrac{OA}{OB}=\dfrac{1}{2}\)
nên \(\widehat{BOA}=60^0\)
Xét ΔOAC có OA=OC và \(\widehat{AOC}=60^0\)
nên ΔOAC đều
=>\(sđ\stackrel\frown{AC}\left(nhỏ\right)=60^0\)
Số đo cung AC lớn là:
\(360-60=300^0\)

a: Xét tứ giác OAO'B có
OA=O'A=O'B=OB=R
nên OAO'B là hình thoi
b: Xét ΔOAO' có OA=O'A=OO'=R
nên ΔOAO' đều
=>\(\widehat{OAO'}=60^0\)
AOBO' là hình thoi
=>\(\widehat{OBO'}=\widehat{OAO'}=60^0\) và \(\widehat{AOB}=\widehat{AO'B}\)
AOBO' là hình thoi
=>\(\widehat{AOB}+\widehat{OAO'}=180^0\)
=>\(\widehat{AOB}=120^0\)
=>\(\widehat{AO'B}=120^0\)
Xét (O) có
\(\widehat{AOB}\) là góc ở tâm chắn cung AB
\(\widehat{AOB}=120^0\)
Do đó: sđ cung nhỏ AB=120 độ
sđ cung lớn AB trong (O) là:
360-120=240 độ
Xét (O') có
\(\widehat{AO'B}=120^0\)
\(\widehat{AO'B}\) là góc ở tâm chắn cung AB
Do đó: sđ cung nhỏ AB=120 độ
sđ cung lớn AB trong (O') là:
360-120=240 độ
c: ΔAOO' đều nên \(S_{AOO'}=\dfrac{AO^2\cdot\sqrt{3}}{4}=R^2\cdot\dfrac{\sqrt{3}}{4}\)
AOBO' là hình thoi
=>\(S_{AOBO'}=2\cdot S_{AOO'}\)
=>\(S_{AOBO'}=2\cdot\dfrac{R^2\sqrt{3}}{4}=\dfrac{R^2\sqrt{3}}{2}\)