Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

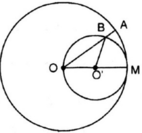

Kiến thức áp dụng
+ Trên đường tròn đường kính R, độ dài cung n0 bằng :
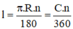

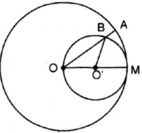
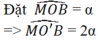 (góc nội tiếp và góc ở tâ của đường tròn (O'))
(góc nội tiếp và góc ở tâ của đường tròn (O'))
Độ dài cung M A ⏜ là:
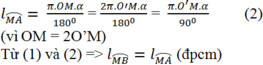

a.
Ta có \(MA=MB\) (t/c hai tiếp tuyến cắt nhau)
\(OA=OB=R\)
\(\Rightarrow OM\) là trung trực AB hay OM vuông góc AB
AC là đường kính và B là điểm thuộc đường tròn \(\Rightarrow\widehat{ABC}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{ABC}=90^0\Rightarrow AB\perp BC\)
\(\Rightarrow BC||OM\) (cùng vuông góc AB)
b.
Do MA là tiếp tuyến \(\Rightarrow AM\perp AC\) hay tam giác MAC vuông tại A
AC là đường kính và K thuộc đường tròn \(\Rightarrow\widehat{AKC}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{AKC}=90^0\) hay AK là đường cao trong tam giác vuông MAC
Áp dụng hệ thức lượng:
\(AC^2=CK.CM\Rightarrow CK.CM=\left(2R\right)^2=4R^2\)
c.
Em có nhầm đề ko nhỉ, vì 2 góc này hiển nhiên bằng nhau, ko cần chứng minh, do 1 góc là góc nội tiếp và 1 góc là góc tạo bởi tiếp tuyến và dây cung, cùng chắn cung BK.

a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
b: Xét ΔOAM vuông tại A có \(sinAMO=\dfrac{OA}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AMO}=30^0\)
Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MO là phân giác của góc AMB
=>\(\widehat{AMB}=2\cdot\widehat{AMO}=60^0\)
Xét ΔMAB có MA=MB và \(\widehat{AMB}=60^0\)
nên ΔMAB đều
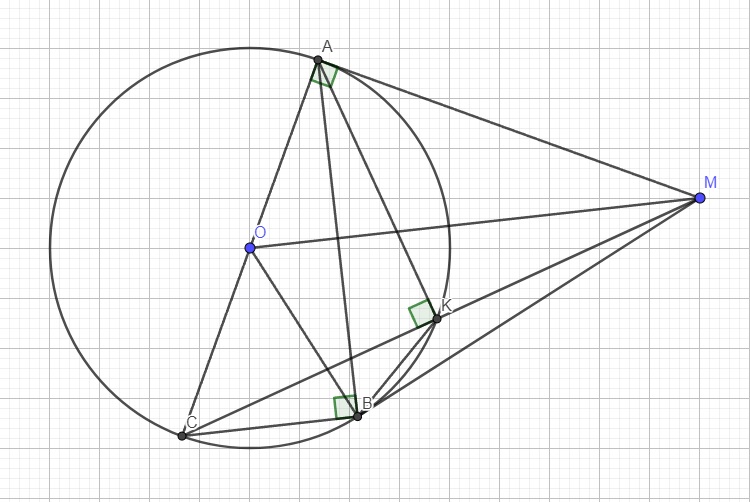
c: Xét (O) có
CA,CP là các tiếp tuyến
Do đó: CA=CP và OC là phân giác của góc AOP
Xét (O) có
DB,DP là các tiếp tuyến
Do đó; DB=DP và OD là phân giác của góc BOP
ΔOAM vuông tại A
=>\(OA^2+AM^2=OM^2\)
=>\(AM^2=\left(2R\right)^2-R^2=3R^2\)
=>\(AM=R\sqrt{3}\)
Chu vi tam giác MCD là:
\(C_{MCD}=MC+CD+MD\)
\(=MC+CP+MD+DP\)
\(=MC+CA+MD+DB\)
=MA+MB=2MA=\(=R\sqrt{3}\cdot2=2R\sqrt{3}\)
d: Ta có: OC là phân giác của góc AOP
=>\(\widehat{AOP}=2\cdot\widehat{COP}\)
Ta có: OD là phân giác của góc BOP
=>\(\widehat{BOP}=2\cdot\widehat{DOP}\)
Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}+\widehat{AMB}+\widehat{AOB}=360^0\)
=>\(\widehat{AOB}+60^0+90^0+90^0=360^0\)
=>\(\widehat{AOB}=120^0\)
Ta có: \(\widehat{AOP}+\widehat{BOP}=\widehat{AOB}\)
=>\(2\cdot\left(\widehat{COP}+\widehat{DOP}\right)=120^0\)
=>\(2\cdot\widehat{COD}=60^0\cdot2\)
=>\(\widehat{COD}=60^0\)
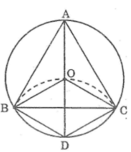

Đặt ˆMOB=αMOB^=α
⇒ˆMO′B=2α⇒MO′B^=2α (góc nội tiếp và góc ở tâm của đường tròn (O’))
Độ dài cung MB là:
lcungMB=π.O′M.2α1800=π.O′M.α900(1)lcungMB=π.O′M.2α1800=π.O′M.α900(1)
Độ dại cung MA là:
lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)
(Vì OM = 2O’M)
Từ (1) và (2) ⇒ sđcung MA = sđcung MB
Đặt ˆMOB=αMOB^=α
⇒ˆMO′B=2α⇒MO′B^=2α (góc nội tiếp và góc ở tâm của đường tròn (O’))
Độ dài cung MB là:
lcungMB=π.O′M.2α1800=π.O′M.α900(1)lcungMB=π.O′M.2α1800=π.O′M.α900(1)
Độ dại cung MA là:
lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)
(Vì OM = 2O’M)
Từ (1) và (2) ⇒ sđcung MA = sđcung MB