Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số sản phẩm làm theo kế hoạch là \(x\) (sản phẩm)
=> Số ngày dự định làm xong là: \(\frac{x}{25}\) (ngày)
Số sản phẩm làm được sau khi cải tiến kĩ thuật là: \(x+10\) (sản phẩm)
=> Số ngày làm xong là: \(\frac{x+10}{30}\) (ngày)
Ta có: \(\frac{x}{25}-\frac{x+10}{30}=3\)
Giải phương trình đi bạn :)

Gọi số sản phẩm mỗi ngày làm được theo dự định của 2 tổ là x (sản phẩm)
Và thời gian làm xong công việc theo dự định là y
Theo đề ra ta có
Tổ 1 làm thêm 4 sản phẩm 1 ngày so với dự định nên xong sớm 3 ngày thừa 58 sản phẩm ta có phương trình
(X+4)(y-3)-58=xy
Suy ra 4y-3x=70(*)
Tổ 2 làm thêm 3 sản phẩm nên xong sớm 3 ngày và thừa 54 sản phẩm ta có pt
(X+3)(y-2)-54=xy
Suy ra 3y-2x=60 (**)
Từ (*),(**) ta có hệ
4y-3x=70 và3y-2x=60
Giải hệ được y=40;x=30
Vậy số sản phẩm cần sản xuất theo dự định là xy=1200

Gọi năng suất ban đầu là x, thời gian ban đầu là y
Theo đề, ta có hệ: xy=120 và 2x+(x+4)(y-2-1)-16=120
=>xy=120 và 2x+(x+4)(y-3)=136
=>xy=120 và 2x+xy-3x+4y-12=136
=>xy=120 và -x+4y+120-12=136
=>-x+4y=28 và xy=120
=>x=4y-28 và y(4y-28)=120
=>y=10 và x=4*10-28=12

Gọi 3 phân xưởng 1,2,3 sản xuất theo thứ tự là a,b,c
ta có \(a=\frac{1}{2}b=2c\) lại có \(a+b+c=630\) (1). Khi \(a=\frac{1}{2}b\Rightarrow b=2a\) (*) . Khi \(a=2c\Rightarrow c=\frac{a}{2}\) (**)
Thay (*) và (**) vào (1) ta có pt : \(a+2a+\frac{a}{2}=630\Leftrightarrow\frac{7}{2}a=630\Leftrightarrow a=180\)
Vậy a=180 ; b=360 ; c=90
Gọi số sản phẩm của phân xưởng 1 là a
số sản phẩm của phân xưởng 2 là b
số sản phẩm của phân xưởng 3 là c
Ta có:
\(a+b+c=630\)
\(2b+2c+c=630\)
\(4c+2c+c=630\)
\(7c=360\)
\(c=\frac{630}{7}\)
\(c=90\)
\(b=2c=2\times90=180\)
\(a=2b=2\times180=360\)
Vậy phân xưởng 1 sản xuất được 360 sản phẩm
phân xưởng 2 sản xuất được 180 sản phẩm
phân xưởng 3 sản xuất được 90 sản phẩm
Chúc bạn học tốt![]()

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II sản xuất ra.
Như vậy tiền lãi có được là L = 3x + 5y (nghìn đồng).
Theo đề bài: Nhóm A cần 2x + 2y máy;
Nhóm B cần 0x + 2y máy;
Nhóm C cần 2x + 4y máy;
Vì số máy tối đa ở nhóm A là 10 máy, nhóm B là 4 máy, nhóm C là 12 máy nên x, y phải thỏa mãn hệ bất phương trình: 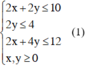
Khi đó bài toán trở thành: trong các nghiệm của hệ bất phương trình (1) thì nghiệm (x = xo; y = yo) nào cho L = 3x + 5y lớn nhất.
Miền nghiệm của hệ bất phương trình (1) là ngũ giác ABCDE kể cả miền trong.
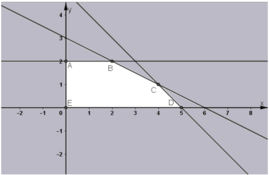
Ta có: L đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác ABCDE.
Tính giá trị của biểu thức L = 3x + 5y tại các đỉnh ta được:
Tại đỉnh A(0;2), L = 10
Tại đỉnh B(2; 2), L = 16
Tại đỉnh C(4; 1), L = 17
Tại đỉnh D(5; 0), L = 15
Tại đỉnh E(0; 0), L = 0.
Do đó, L = 3x + 5y lớn nhất là 17 (nghìn đồng) khi: x = 4; y = 1
Vậy để có tiền lãi cao nhất, cần sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm loại II.

Gọi thời gian làm riêng của máy 1;2;3 lần lượt là a,b,c
Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b+c=95\\2c-a-b=10\\a=7b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{105}{2}\left(loại\right)\\b=\dfrac{15}{2}\left(loại\right)\\c=35\left(nhận\right)\end{matrix}\right.\)
=>Đề sai rồi bạn, số máy làm sao là số thập phân được