Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi năng suất ban đầu là x, thời gian ban đầu là y
Theo đề, ta có hệ: xy=120 và 2x+(x+4)(y-2-1)-16=120
=>xy=120 và 2x+(x+4)(y-3)=136
=>xy=120 và 2x+xy-3x+4y-12=136
=>xy=120 và -x+4y+120-12=136
=>-x+4y=28 và xy=120
=>x=4y-28 và y(4y-28)=120
=>y=10 và x=4*10-28=12
Gọi x (ngày) là số ngày dự định làm xong kế hoạch (x > 0).
Khi đó:
Số sản phẩm dự định làm trong một ngày là: 360/x (sản phẩm)
Thực tế, mỗi ngày làm thêm được 9 sản phẩm nên năng suất thực tế là: 360/x + 9 (sản phẩm / ngày)
Số ngày làm thực tế là: x – 1 (ngày)
Số sản phẩm làm được trong x – 1 ngày là: 360 + 360.5% = 378 sản phẩm.
Ta có phương trình:
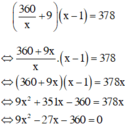
⇔ x = 8 (thỏa mãn) hoặc x = –5 (loại)
Số ngày dự định là 8 ngày, năng suất thực tế là 360:8 + 9 = 54 sản phẩm/ngày
Vậy khi đến hạn, phân xưởng sẽ làm được 54.8 = 432 sản phẩm.
Gọi x là số sản phẩm sản xuất trong một ngày theo định mức.
Điều kiện x nguyên dương. Theo đề ta có chương trình:
\(\dfrac{360}{x}=\dfrac{360+\dfrac{360.5}{100}}{x+9}+1\)
⇔ x2 + 27x – 3240 = 0
⇒ x1= -72 (loại), x2 = 45.
Thời gian giao hoàn thành kế hoạch là = 8 ngày
Nếu sản xuất theo thời gian đã định với năng suất mới thì số sản phẩm làm được là (45+9).8=432 sản phẩm.
Chọn B
Gọi x; y lần lượt là số cái bánh đậu xanh, bánh dẻo . Khi đó; số tiền lãi là L= 2x+ 1,8 y
Bài toán trở thành tìm số tự nhiên x; y thoả mãn hệ
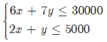sao cho L= 2x+ 1,8 y lớn nhất.
Từ đó ta có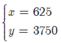 
thì L đạt giá trị lớn nhất.
Vậy cần 625 bánh đậu xanh và 3750 bánh dẻo thì lãi lớn nhất.
Gọi thời gian làm riêng của máy 1;2;3 lần lượt là a,b,c
Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b+c=95\\2c-a-b=10\\a=7b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{105}{2}\left(loại\right)\\b=\dfrac{15}{2}\left(loại\right)\\c=35\left(nhận\right)\end{matrix}\right.\)
=>Đề sai rồi bạn, số máy làm sao là số thập phân được