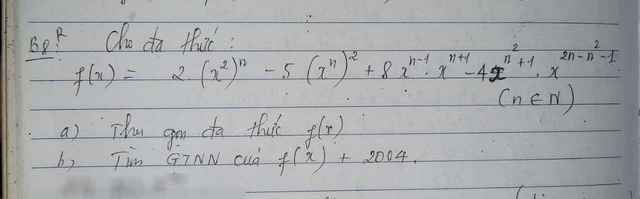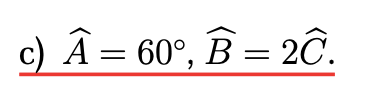NT
Giúp mình làm mấy câu tô màu vàng được ko ạ?Mình cảm ơn ạ!
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 1 2022
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{KAC}\) chung
Do đó: ΔABH=ΔACK
Suy ra: AH=AK
b: Xét ΔKIB vuông tại K và ΔHIC vuông tại H có
KB=HC
\(\widehat{KBI}=\widehat{HCI}\)
Do đó: ΔKIB=ΔHIC
Suy ra: IK=IH
Xét ΔAKI vuông tại K và ΔAHI vuông tại H có
AI chung
KI=HI
Do đó: ΔAKI=ΔAHI
Suy ra: \(\widehat{KAI}=\widehat{HAI}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2022
Do số đã cho là số lẻ nên ko chia hết cho 2
Do số đã cho có tận cùng khác 0, 5 nên ko chia hết cho 5
Gọi p là 1 số nguyên tố nào đó, với \(p\ne\left\{2;5\right\}\) \(\Rightarrow2^x.5^y\) nguyên tố cùng nhau p
\(\Rightarrow10^z\) nguyên tố cùng nhau với p với mọi z nguyên dương
Ta xét dãy gồm p+1 số có dạng:
1; 11; 111; ...; 111...11 (p+1 chữ số 1)
Theo nguyên lý Dirichlet, trong p+1 số trên có ít nhất 2 số có cùng số dư khi chia hết cho p
Giả sử đó là 111..11 (m chữ số 1) và 111...11 (n chữ số 1), với \(m< n\le p\)
\(\Rightarrow111...11\left(n\text{ chữ số 1}\right)-111...11\left(m\text{ chữ số 1}\right)\) chia hết cho p
\(\Rightarrow111...11000...00\left(a\text{ chữ số 1}\text{ và b chữ số 0}\right)\) chia hết cho p (với a<m)
\(\Rightarrow111...11.10^b\) chia hết cho p
Mà \(10^p\) nguyê tố cùng nhau với p
\(\Rightarrow111...11\left(a\text{ chữ số 1}\right)\) chia hết cho p
Vậy với mọi số nguyên tố p khác 2 và 5, luôn luôn tìm được ít nhất 1 số có dạng 111...11 chia hết cho p
\(\Rightarrow\) Mọi số nguyên tố, trừ 2 và 5, đều có thể là ước của số có dạng 111...11
ND
0
BP
3
TD
1
31 tháng 10 2021
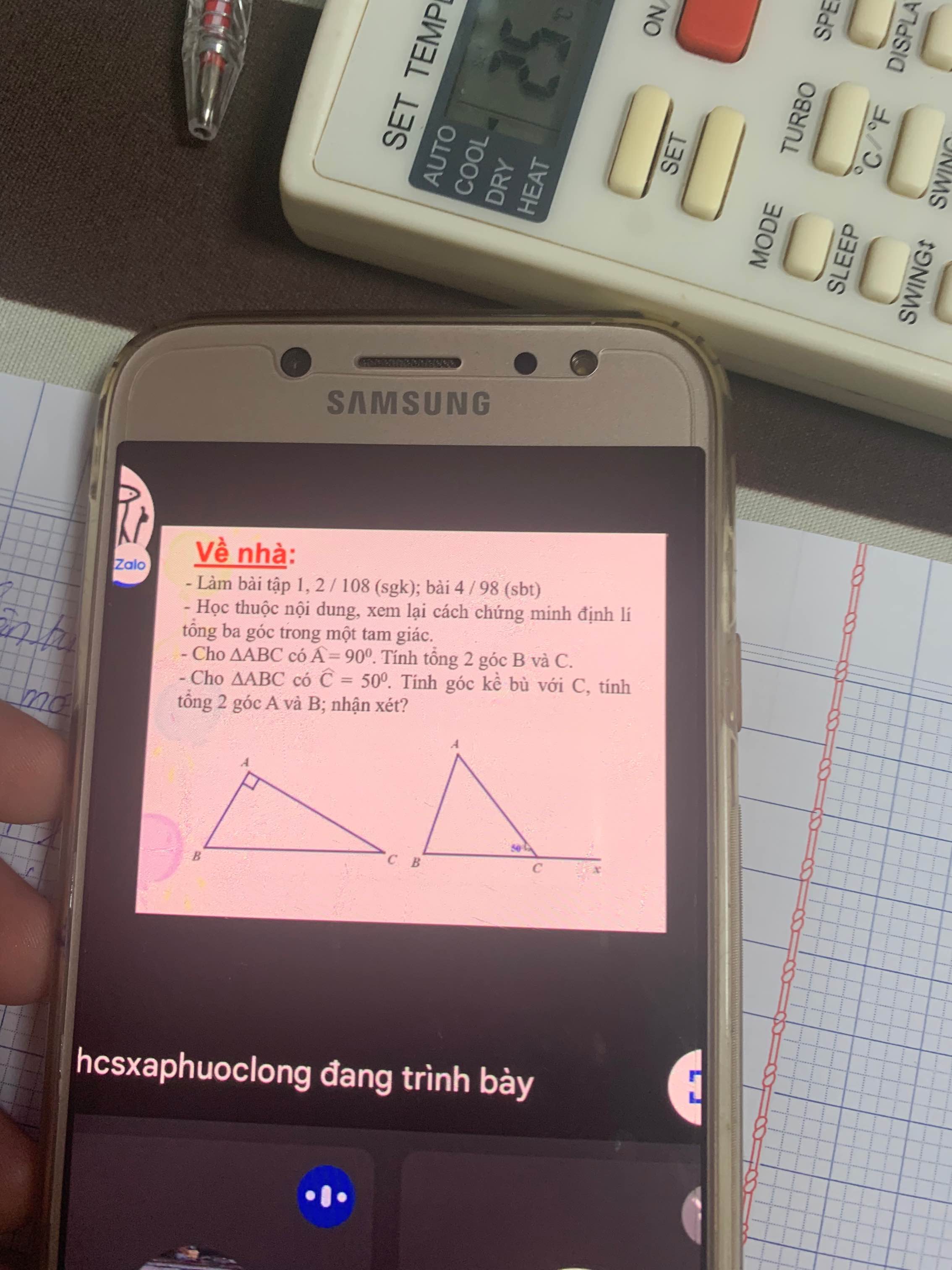
a: \(\widehat{B}+\widehat{C}=90^0\)
c: Góc kề bù với C bằng tổng của góc A cộng góc B