
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


BT1.
Ta có: \(2009^{20}=2009^{10}\times2009^2\)và \(20092009^{10}=2009^{10}\times10001^{10}\)
Rõ ràng \(2009^2< 10001^{10}\\ \Rightarrow2009^{10}\times2009^2< 2009^{10}\times10001^{10}\\ \Rightarrow2009^{20}< 20092009^{10}\left(đpcm\right)\)
BT9. Bn xem lại đề bài đi. \(x^2+x+1\) luôn lớn hơn 0 mà bn.
BT3.
Giả sử \(M\in N\)
Nên:
\(\left\{{}\begin{matrix}\dfrac{x}{x+y+z}\in N\\\dfrac{y}{y+x+t}\in N\\\dfrac{z}{z+t+y}\in N\\\dfrac{t}{t+z+x}\in N\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x⋮x+y+z\\y⋮y+x+t\\z⋮z+t+y\\t⋮t+z+x\end{matrix}\right.\)
Vì \(x,y,z,t\in N\)*\(\Rightarrow x,y,z,t>0\)\(\Rightarrow\left\{{}\begin{matrix}x>x+y+z\\y>x+y+t\\z>y+z+t\\t>x+z+t\end{matrix}\right.\)(vô lí)
Vậy rõ ràng điều giả sử là vô lí. Nên \(M\notin N\left(đpcm\right)\)
Mình chỉ giúp đc đến đây thôi, mong bn thông cảm
Ngoài ra, chúc bn học tốt nhé![]()
![]()
![]()
![]()
![]()
Bài toán 2.
Ta có: \(B=\dfrac{2008}{1}+\dfrac{2007}{2}+\dfrac{2006}{3}+....+\dfrac{2}{2007}+\dfrac{1}{2008}\)
\(=\dfrac{2009-1}{1}+\dfrac{2009-2}{2}+\dfrac{2009-3}{3}+...+\dfrac{2009-2008}{2008}\)
\(=2009-1+\dfrac{2009}{2}-1+\dfrac{2009}{3}-1+....+\dfrac{2009}{2008}-1\)
\(=2009+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{....1}{2008}\right)-1.2008\)
\(=\left(2009-2008\right)+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=1+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2008}+\dfrac{1}{2009}\right)\)
=\(2009.A\)
Do đó, tỉ số \(\dfrac{A}{B}=\dfrac{A}{2009.A}=\dfrac{1}{2009}\)



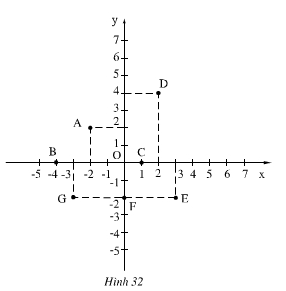
Ta có tọa độ các điểm: A(-2; 2); B(-4; 0); C(1; 0); D(2; 4); E(3; -2); F(0; -2); G(-3; -2)

| Giá trị (x) | Tần số (n) | Các tích (x.n) | |
| 17 | 3 | 51 | |
| 18 | 5 | 90 | |
| 19 | 4 | 76 | |
| 20 | 2 | 40 | |
| 21 | 3 | 63 | |
| 22 | 2 | 44 | |
| 24 | 3 | 72 | |
| 26 | 3 | 78 | |
| 28 | 1 | 28 | |
| 30 | 1 | 30 | |
| 31 | 2 | 62 | |
| 32 | 1 | 32 | |
| N = 30 | Tổng: 666 |















 Giúp mình làm mấy câu tô màu vàng được ko ạ?Mình cảm ơn ạ!
Giúp mình làm mấy câu tô màu vàng được ko ạ?Mình cảm ơn ạ!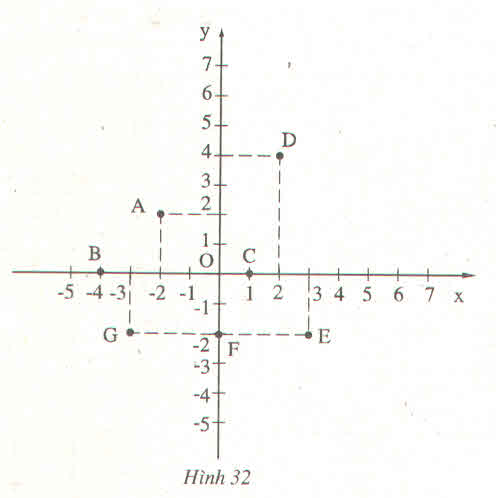

a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{KAC}\) chung
Do đó: ΔABH=ΔACK
Suy ra: AH=AK
b: Xét ΔKIB vuông tại K và ΔHIC vuông tại H có
KB=HC
\(\widehat{KBI}=\widehat{HCI}\)
Do đó: ΔKIB=ΔHIC
Suy ra: IK=IH
Xét ΔAKI vuông tại K và ΔAHI vuông tại H có
AI chung
KI=HI
Do đó: ΔAKI=ΔAHI
Suy ra: \(\widehat{KAI}=\widehat{HAI}\)