
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔABC có AB<AC<BC(3cm<4cm<5cm)
mà góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
Xét ΔABC có
HB là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB<AC
Do đó: HB<HC
c) Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔCAB=ΔCAD(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔCBD có CB=CD(cmt)
nên ΔCBD cân tại C(Định nghĩa tam giác cân)


a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
SUy ra: AB//CD

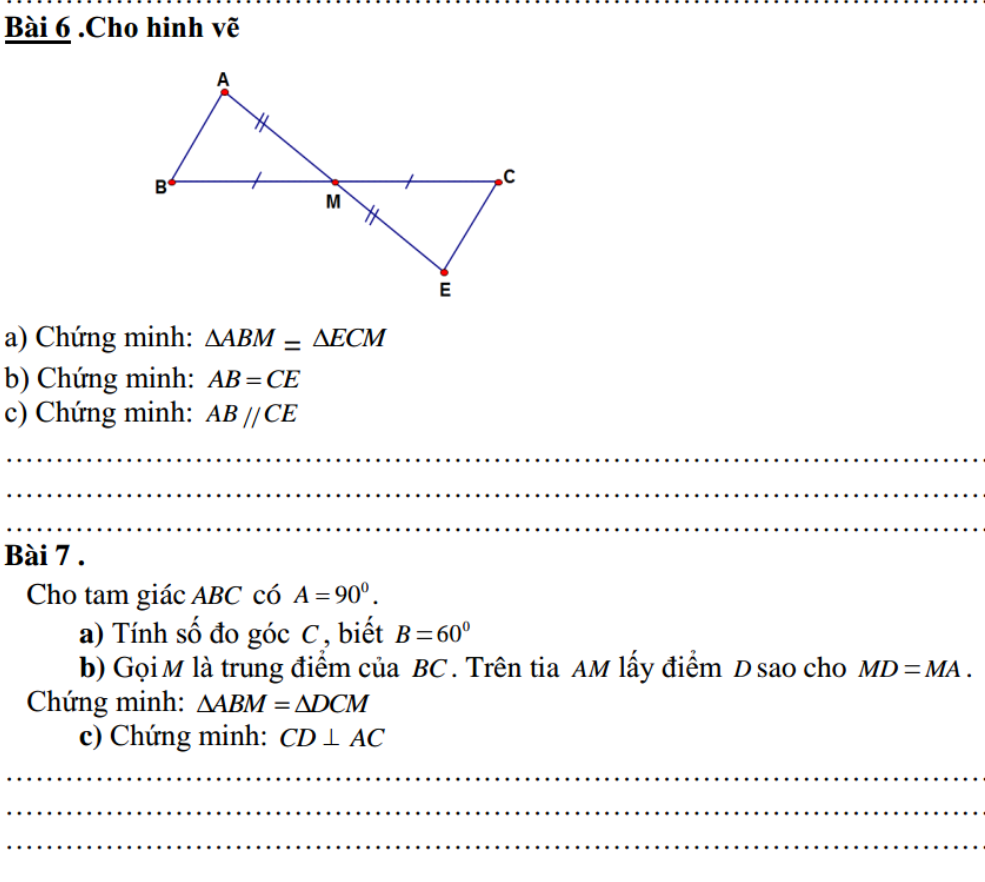
a, Xét tam giác ABM và tam giác ECM
^AMB = ^EMC ( đối đỉnh )
BM = MC ( gt )
AM = ME ( gt )
Vậy tam giác ABM = tam giác ECM ( c.g.c )
b, Vì tam giác ABM = tam giác ECM ( cma )
=> AB = EC
c, Vì tam giác ABM = tam giác ECM ( cma )
=> ^ABM = ^ECM
mà 2 góc này ở vị trí so le trong => AB // CE


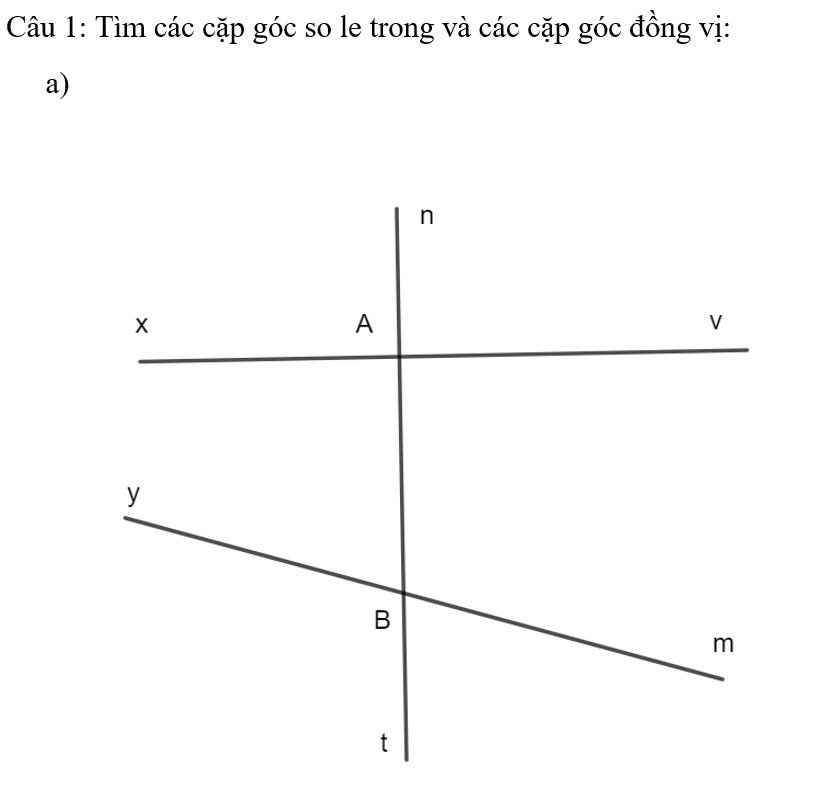
a: So le trong: góc vAB và góc yBA; góc xAB và góc mBA
ĐỒng vị: góc nAx và góc yBA; góc nAv và góc mBA; góc xAB và góc tBy; góc vAB và góc mBt
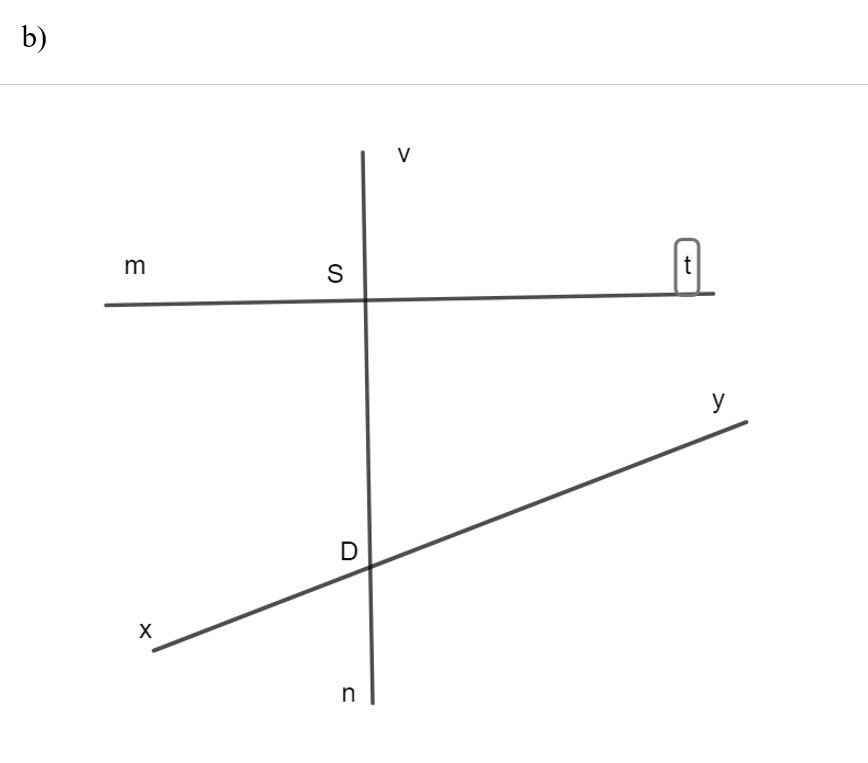
b: So le trong: góc mSD và góc yDS; góc tSD và góc xDS
ĐỒng vị: góc vSm và góc xDv; góc vSt và góc vDy; góc mSn và góc xDn; góc tSD và góc yDn
a)Cặp so le trong: xAB và ABm, vAB và ABy
Cặp đồng vị: nAx và ABy, nAv và ABm, xAB và yBt,vAB và mBt
b)Cặp so le trong: mSD và SDy, tSD và SDx
Cặp đồng vị: vSm và SDx, vSt và SDy, nDx và DSm,nDy và DSt

a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{KAC}\) chung
Do đó: ΔABH=ΔACK
Suy ra: AH=AK
b: Xét ΔKIB vuông tại K và ΔHIC vuông tại H có
KB=HC
\(\widehat{KBI}=\widehat{HCI}\)
Do đó: ΔKIB=ΔHIC
Suy ra: IK=IH
Xét ΔAKI vuông tại K và ΔAHI vuông tại H có
AI chung
KI=HI
Do đó: ΔAKI=ΔAHI
Suy ra: \(\widehat{KAI}=\widehat{HAI}\)

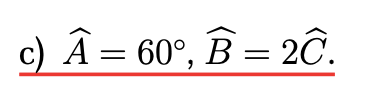

 Giúp mình làm mấy câu tô màu vàng được ko ạ?Mình cảm ơn ạ!
Giúp mình làm mấy câu tô màu vàng được ko ạ?Mình cảm ơn ạ!

Đề bị thiếu điều kiện rồi nên không giải được em nhé!