K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 9 2021
\(A=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\right)\left(1-\dfrac{1}{\sqrt{x}}\right)\left(đk:x>0,x\ne1\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
\(=\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}=\dfrac{4}{\sqrt{x}+1}\)
HP
3 tháng 9 2021
ĐK: \(x\ge0\)
TH1: \(m\le0\Rightarrow\) phương trình vô nghiệm.
TH2: \(m>0\)
\(pt\Leftrightarrow\sqrt{x}+2=\dfrac{6}{m}\)
\(\Leftrightarrow\sqrt{x}=\dfrac{6-2m}{m}\)
Phương trình có nghiệm khi: \(\dfrac{6-2m}{m}\ge0\Leftrightarrow6-2m\ge0\Leftrightarrow m\le3\).
\(\Rightarrow0< m\le3\)
Mà \(m\in Z\Rightarrow m\in\left\{1;2;3\right\}\).
3 tháng 9 2021
\(P=\dfrac{6}{\sqrt{x}+2}\left(đk:x\ge0\right)=m\in Z\)
\(\Rightarrow\sqrt{x}+2\inƯ\left(6\right)=\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
\(\Rightarrow x\in\left\{0;1;16\right\}\)
\(\Rightarrow m\in\left\{1;2;3\right\}\)
5 tháng 9 2021
a: Xét (O) có
ΔABC nội tiếp đường tròn
AB là đường kính
Do đó: ΔBAC vuông tại C
25 tháng 10 2021
Bài 1:
a: ĐKXĐ: \(x\ge0\)
b: \(B=\left(\sqrt{3}-1\right)^2+\dfrac{24-2\sqrt{3}}{\sqrt{2}-1}\)
\(=4-2\sqrt{3}+24\sqrt{2}+24-2\sqrt{6}-2\sqrt{3}\)
\(=28-2\sqrt{6}+24\sqrt{2}-4\sqrt{3}\)
AH
Akai Haruma
Giáo viên
16 tháng 6 2021
Bài 4:
Gọi giá niêm yết 1 chiếc tủ lạnh là $a$ (đồng)
Theo bài ra ta có:
$(2.7500000+a)(1-0,08)=27140000$
$\Rightarrow a=14500000$ (đồng)
AH
Akai Haruma
Giáo viên
16 tháng 6 2021
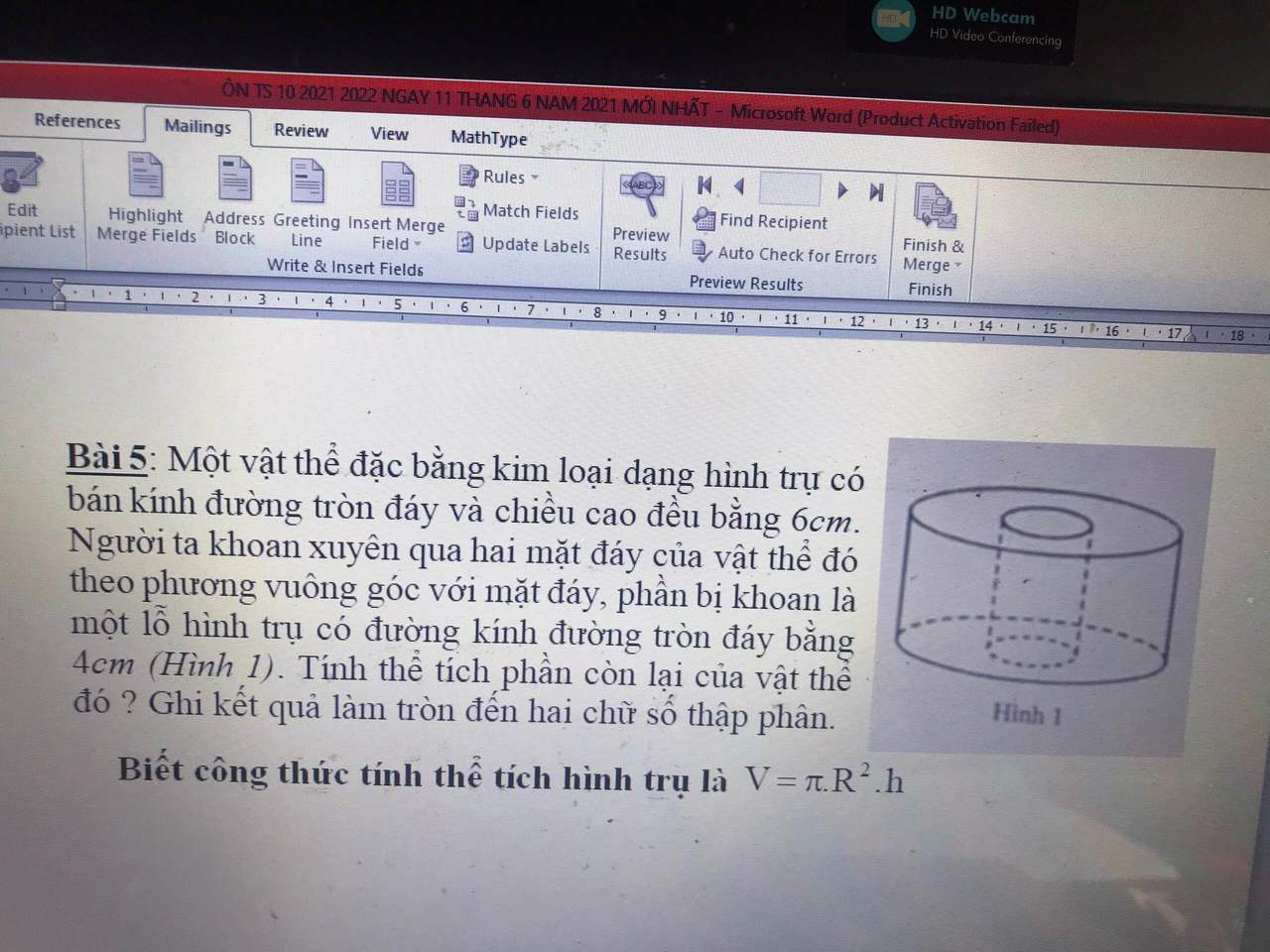
Bài 5:
Theo bài ra thì $r_1=h=6$ (cm)
$r_2=4$ (cm)
Thể tích phần còn lại:
$\pi r_1^2h-\pi r_2^2h=\pi h(r_1^2-r_2^2)$
$=\pi .6(6^2-4^2)=120\pi$ (cm2)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 6 2021
Ta có:
\(\left(\dfrac{a^3}{b^3+c^3}+\dfrac{b^3}{c^3+a^3}+\dfrac{c^3}{a^3+b^3}\right)\left(1+1+1\right)\left(1+1+1\right)\ge\left(\sqrt[3]{\dfrac{a^3}{b^3+c^3}}+\sqrt[3]{\dfrac{b^3}{c^3+a^3}}+\sqrt[3]{\dfrac{c^3}{a^3+b^3}}\right)^3\)
\(\Leftrightarrow\sqrt[3]{\dfrac{a^3}{b^3+c^3}}+\sqrt[3]{\dfrac{b^3}{c^3+a^3}}+\sqrt[3]{\dfrac{c^3}{a^3+b^3}}\le\sqrt[3]{9\left(\dfrac{a^3}{b^3+c^3}+\dfrac{b^3}{c^3+a^3}+\dfrac{c^3}{a^3+b^3}\right)}\)
\(< \sqrt[3]{9\left(\dfrac{2a^3}{a^3+b^3+c^3}+\dfrac{2b^3}{a^3+b^3+c^3}+\dfrac{2c^3}{a^3+b^3+c^3}\right)}=\sqrt[3]{18}< \sqrt[3]{32}=2\sqrt[3]{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 8 2021
\(T=\left(\dfrac{x}{2}+\dfrac{y}{2}-\dfrac{x\sqrt{y}+y\sqrt{x}}{x+y}+\dfrac{3}{4}\right)\left(4040+\dfrac{x}{y}+\dfrac{y}{x}\right)\)
\(T\ge\left(\dfrac{x}{2}+\dfrac{y}{2}-\dfrac{x\sqrt{y}+y\sqrt{x}}{2\sqrt{xy}}+\dfrac{3}{4}\right)\left(4040+\dfrac{x}{y}+\dfrac{y}{x}\right)\)
\(T\ge\left(\dfrac{x}{2}+\dfrac{y}{2}-\dfrac{\sqrt{x}}{2}-\dfrac{\sqrt{y}}{2}+\dfrac{3}{4}\right)\left(4040+2\sqrt{\dfrac{xy}{xy}}\right)\)
\(T\ge\left[\dfrac{1}{2}\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{1}{2}\left(\sqrt{y}-\dfrac{1}{2}\right)^2+\dfrac{1}{2}\right].4042\)
\(T\ge\dfrac{4042}{2}=2021\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 7 2021
\(\Leftrightarrow\dfrac{a+b+c}{a}\left[\dfrac{\left(a+b+c\right)^2-4b\left(a+c\right)}{b\left(a+c\right)}\right]\ge\dfrac{c\left(4a+4c-5b\right)}{b\left(a+c\right)}\)
\(\Leftrightarrow\left(a+b+c\right)\left(a-b+c\right)^2\ge ac\left[4\left(a+c\right)-5b\right]\)
- Nếu \(4\left(a+c\right)\le5b\) BĐT hiển nhiên đúng
- Nếu \(4\left(a+c\right)>5b\)
Do \(ac\le\dfrac{1}{4}\left(a+c\right)^2\) nên ta chỉ cần chứng minh:
\(\left(a+b+c\right)\left(a+c-b\right)^2\ge\dfrac{1}{4}\left(a+c\right)^2\left[4\left(a+c\right)-5b\right]\)
Đặt \(\left\{{}\begin{matrix}a+c=x>0\\b=y>0\end{matrix}\right.\)
\(\Rightarrow4\left(x+y\right)\left(x-y\right)^2\ge x^2\left(4x-5y\right)\)
\(\Leftrightarrow x^2y-4xy^2+4y^3\ge0\)
\(\Leftrightarrow y\left(x-2y\right)^2\ge0\) (luôn đúng)
Dấu "=" xảy ra khi \(x=2y\) hay \(a=b=c\)
AT
11 tháng 6 2021
3a) \(\Delta'=\left(m-1\right)^2-m^2+3m-2=m-1\)
Để pt có 2 nghiệm phân biệt thì \(\Delta>0\Rightarrow m>1\)
b) Áp dụng hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-3m+2\end{matrix}\right.\)
Theo đề: \(x_1^2+x_2^2=3x_1x_2\Rightarrow\left(x_1+x_2\right)^2=5x_1x_2\)
\(\Rightarrow4\left(m-1\right)^2=5m^2-15m+10\Rightarrow m^2-7m+6=0\)
\(\Rightarrow\left(m-1\right)\left(m-6\right)=0\Rightarrow\left[{}\begin{matrix}m=1\\m=6\end{matrix}\right.\) mà \(m>1\Rightarrow m=6\)
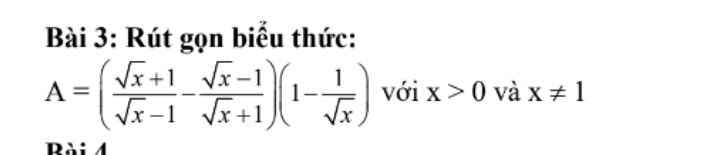
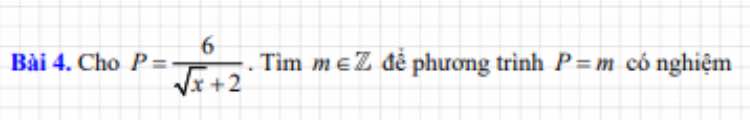
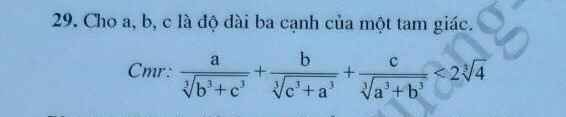
Bài 2:
a) ĐKXĐ: \(x\ge1\)
\(pt\Leftrightarrow x^2-4x+5=x^2-2x+1\)
\(\Leftrightarrow2x=4\Leftrightarrow x=2\left(tm\right)\)
b) ĐKXĐ: \(x\le\dfrac{16}{5}\)
\(pt\Leftrightarrow-5x+16=24\Leftrightarrow5x=-8\Leftrightarrow x=-\dfrac{8}{5}\left(tm\right)\)
c) ĐKXĐ: \(x\ge0\)
\(pt\Leftrightarrow5x=2+x\Leftrightarrow4x=2\Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
d) \(pt\Leftrightarrow\sqrt{\left(x-2\right)^2}=8\)
\(\Leftrightarrow\left|x-2\right|=8\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=8\\x-2=-8\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=10\\x=-6\end{matrix}\right.\)