MT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
2
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
1.
Xét pt đầu:
\(x^2-xy+x-y=0\)
\(\Leftrightarrow x\left(x-y\right)+x-y=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-y\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=y\end{matrix}\right.\)
TH1: \(x=-1\) thay xuống pt dươi:
\(\sqrt{y^2+15}=-3-2+\sqrt{9}\Leftrightarrow\sqrt{y^2+15}=-2< 0\) (vô nghiệm)
TH2: thay \(y=x\) xuống pt dưới:
\(\sqrt{x^2+15}=3x-2+\sqrt{x^2+8}\) (1)
\(\Rightarrow3x-2=\sqrt{x^2+15}-\sqrt{x^2+8}=\dfrac{7}{\sqrt{x^2+15}+\sqrt{x^2+8}}>0\)
\(\Rightarrow x>\dfrac{2}{3}\)
Do đó (1) tương đương:
\(3x-2+\sqrt{x^2+8}-\sqrt{x^2+15}=0\)
\(\Leftrightarrow3x-3+\sqrt{x^2+8}-3+4-\sqrt{x^2+15}=0\)
\(\Leftrightarrow3\left(x-1\right)+\dfrac{\left(x-1\right)\left(x+1\right)}{\sqrt{x^2+8}+3}-\dfrac{\left(x-1\right)\left(x+1\right)}{\sqrt{x^2+15}+4}=0\)
\(\Leftrightarrow\left(x-1\right)\left[3+\left(x+1\right)\left(\dfrac{1}{\sqrt{x^2+8}+3}-\dfrac{1}{\sqrt{x^2+15}+4}\right)\right]=0\)
\(\Leftrightarrow x-1=0\) (do \(x+1>0\) nên ngoặc phía sau luôn dương)
\(\Leftrightarrow x=y=1\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
2.
Pt đầu tương đương:
\(y^2-x+x^2-2xy+x=0\)
\(\Leftrightarrow\left(x-y\right)^2=0\Leftrightarrow y=x\)
Thay xuống pt dưới:
\(2x^2+x-x^2+x-3=0\)
\(\Leftrightarrow x^2+2x-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-3\Rightarrow y=-3\end{matrix}\right.\)
NT
1
24 tháng 7 2021
3) Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(m^2-6\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-6\right)\)
\(=4m^2-8m+4-4m^2+24\)
\(=-8m+28\)
Để phương trình có hai nghiệm phân biệt x1;x2 thì Δ>0
\(\Leftrightarrow-8m+28>0\)
\(\Leftrightarrow-8m>-28\)
hay \(m< \dfrac{7}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{1}=2m-2\\x_1x_2=m^2-6\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=16\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(m^2-6\right)-16=0\)
\(\Leftrightarrow4m^2-8m+4-2m^2+12-16=0\)
\(\Leftrightarrow2m^2-8m=0\)
\(\Leftrightarrow2m\left(m-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\left(nhận\right)\\m=4\left(loại\right)\end{matrix}\right.\)
1D
2
KN
0
3 tháng 10 2021
câu 4:
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\)
hay AH=6(cm)
b: Xét ΔBAC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
nên \(AM=\dfrac{BC}{2}=6.5\left(cm\right)\)
NQ
0
DT
22 tháng 12 2021
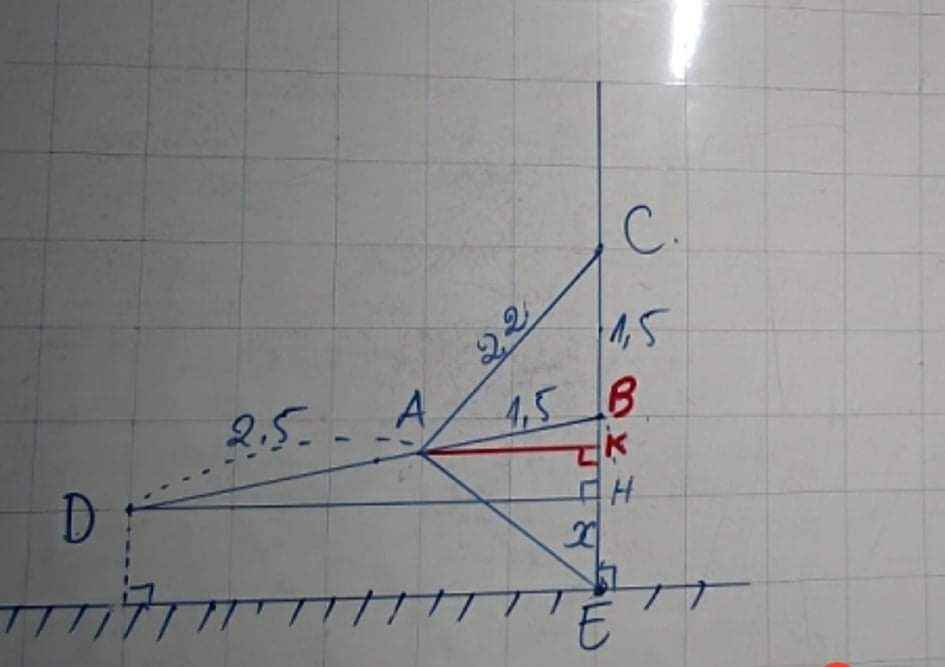
Gọi DH là khoảng cách thấp nhất từ máy bay đến mặt đất, khi đó AC có độ dài lớn nhất là 2,2m. Dựng hình chữ nhật DHEK => DH = EK
Do BA = BE = BC = 1,5m cố định nên tam giác ACE vuông tại A
Xét tam giác ACE vuông tại A có cos\(\widehat{ECA}\) = \(\dfrac{CA}{CE}=\dfrac{2,2}{3}\) => \(\widehat{ECA}\) \(\approx\) 42o50'
BA = BC => tam giác ABC cân tại B => \(\widehat{BAC}=\widehat{BCA}\) = \(\widehat{ECA}\) \(\approx\) 42o50'
=> \(\widehat{DBK}\) = \(\widehat{BAC}+\widehat{BCA}\) = 2.\(\widehat{BCA}\) = 85o40'
Xét tam giác DBK vuông tại D có: BK = BD. cos\(\widehat{DBK}\)
= 4.cos85o40' \(\approx\) 0,3022
=> DH = KE \(\approx\) 1,5 - 0,3022 \(\approx\)1,2 (m)
Chỉ cách bấm máy tính ấy vì bài này giải bằng máy tính
tìm trên gg đi