
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{x}{y}=\frac{y}{z}=\frac{z}{t}=\frac{x+y+z}{y+z+t}\)
\(\Rightarrow\frac{x^3}{y^3}=\frac{y^3}{z^3}=\frac{z^3}{t^3}=\frac{\left(x+y+z\right)^3}{\left(y+z+t\right)^3}=\left(\frac{x+y+z}{y+z+t}\right)^3=\frac{x}{y}.\frac{y}{z}.\frac{z}{t}=\frac{z}{t}\)
Vậy ..

5:
=10x^3*1/2xy-2/5y*1/2xy+1/2z*1/2xy
=5x^3y-1/5xy^2+1/4xyz
6: =x^2y*4xy+x^2y*3y-5x*x^2y
=4x^3y^2+3x^2y^2-5x^3y
7: =-4/3xy*3x^2y+4/3xy*6xy-4/3xy*9x
=-4x^3y^2+8x^2y^2-12x^2y

Đây bn nhé:
Ta có a/3 = b/8= c/5. Áp dụng tính chất dãy tỉ số bằng nhau ta có:
2a+3b-c/2.3+3.8-5 = 2a+3b-c/6+24-5 = 50/25 = 2
=> a/3 = 2 => a=6
=> b/8 = 2 => b=16
=> c/5 = 2 => c=10
Nhìn ngắn vậy thôi chứ ko sai đâu bn
Chúc bn học tốt^^
\(\dfrac{a}{3}\) = \(\dfrac{b}{8}\) = \(\dfrac{c}{5}\) và 2a + 3b - c = 50
=> \(\dfrac{2a}{6}\) = \(\dfrac{3b}{24}\) = \(\dfrac{c}{5}\) và 2a + 3b - c = 50
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{2a}{6}\) = \(\dfrac{3b}{24}\) = \(\dfrac{c}{5}\) = \(\dfrac{2a+3b-c}{6+24-5}\) = \(\dfrac{50}{25}\) = 2
Vậy:
\(\dfrac{2a}{6}=2\) => \(2a=2.6=12\) => \(a=12:2=6\)
\(\dfrac{3b}{24}=2\) => \(3b=2.24=48\) => \(b=48:3=16\)
\(\dfrac{c}{5}=2\) => \(c=2.5=10\)

Bài 8:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó:ΔABM=ΔACM
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: ME=MF
hay ΔMEF cân tại M

Muốn tạo số chia hết cho 4 thì 2 chữ số tận cùng phải chia hết cho 4
Gọi các số cần tìm có dạng \(\overline{abc}\left(a,b,c\in N;0< a< 10;0\le b,c< 10\right)\)
Mà \(\overline{abc}⋮4\Rightarrow\overline{bc}\in\left\{00;04;12;16;20;24;40;44;60;64\right\}\)
Với mỗi cặp \(\overline{bc}\) ta có \(a\in\left\{1;2;4;6\right\}\left(4\text{ cách chọn}\right)\)
Vậy có thể tạo \(4\cdot10=40\) số thỏa yêu cầu đề

\(\left|x+\dfrac{1}{7}\right|-\dfrac{2}{3}=0\)
\(\Rightarrow\left|x+\dfrac{1}{7}\right|=0+\dfrac{2}{3}\\ \Rightarrow\left|x+\dfrac{1}{7}\right|=\dfrac{2}{3}\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{1}{7}=\dfrac{2}{3}\\x+\dfrac{1}{7}=-\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}-\dfrac{1}{7}\\x=-\dfrac{2}{3}-\dfrac{1}{7}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{11}{21}\\x=-\dfrac{17}{21}\end{matrix}\right.\)

3A=1.2.(3-0)+2.3.(4-1)+...+n(n+1)[(n-1)(n+2)]
3A=1.2.3-0.1.2+2.3.4-1.2.3+...n.(n+1)(n+2)-(n-1)n(n+1)
A=n(n+1)(n+2):3

Bài 3:
theo đề bài ta có:
\(\left\{{}\begin{matrix}2a-3b=0\\5b-7c=0\\3a-7b+5c=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=42\\b=28\\c=20\end{matrix}\right.\)
Bài 4:
Đặt \(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{6}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k\\y=5k\\z=6k\end{matrix}\right.\)
Ta có: \(x^2-2y^2+z^2=18\)
\(\Leftrightarrow16k^2-50k^2+36k^2=18\)
\(\Leftrightarrow k^2=9\)
Trường hợp 1: k=3
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=4\cdot3=12\\y=5k=5\cdot3=15\\z=6k=6\cdot3=18\end{matrix}\right.\)
Trường hợp 2: k=-3
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=-3\cdot4=-12\\y=5k=-3\cdot5=-15\\z=6k=-3\cdot6=-18\end{matrix}\right.\)





 giúp em câu này nữa ạ, làm phiền mấy anh chị rồi ạ, xl :)
giúp em câu này nữa ạ, làm phiền mấy anh chị rồi ạ, xl :)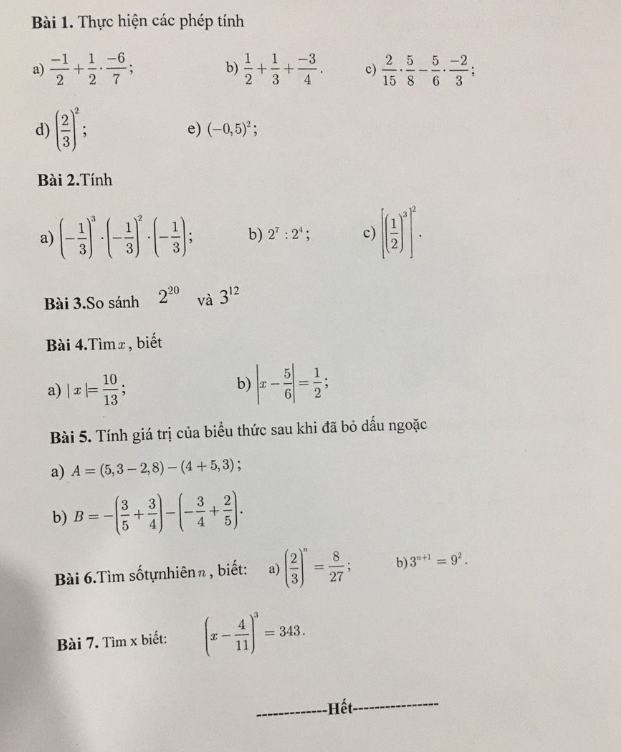
Gọi 3 đơn vị góp vốn lần lượt là: \(a,b,c\left(a,b,c\ne0\right)\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{c}{10}=\dfrac{a+b+c}{5+7+10}=\dfrac{330000000}{22}=15000000\\\)
Khi đó:
\(\dfrac{a}{5}=15000000\Rightarrow a=15000000.5=75000000\)
\(\dfrac{b}{7}=15000000\Rightarrow b=15000000.7=105000000\)
\(\dfrac{c}{10}=15000000\Rightarrow c=15000000.10=150000000\)