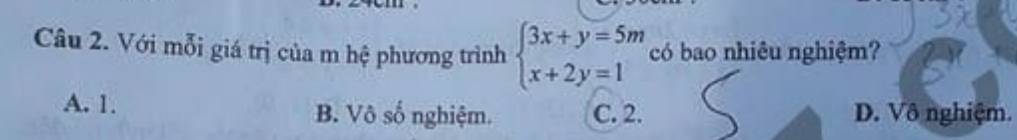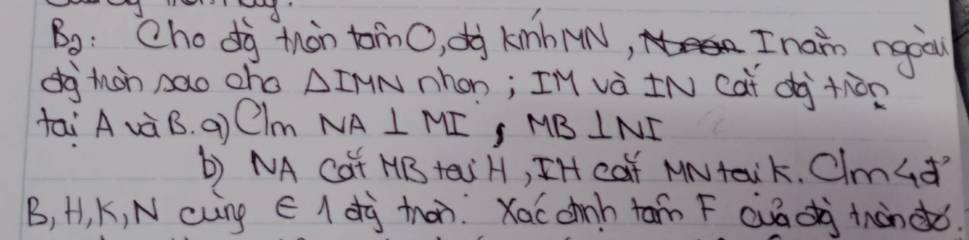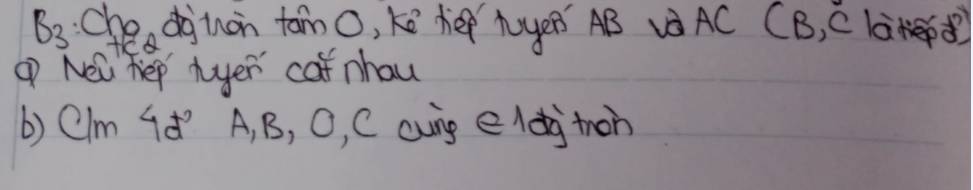HA
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 12 2023
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA tại C
=>CB\(\perp\)AF tại C
Xét tứ giác BHCF có \(\widehat{BHF}=\widehat{BCF}=90^0\)
nên BHCF là tứ giác nội tiếp
=>B,H,C,F cùng thuộc một đường tròn
NP
1
5 tháng 4 2023
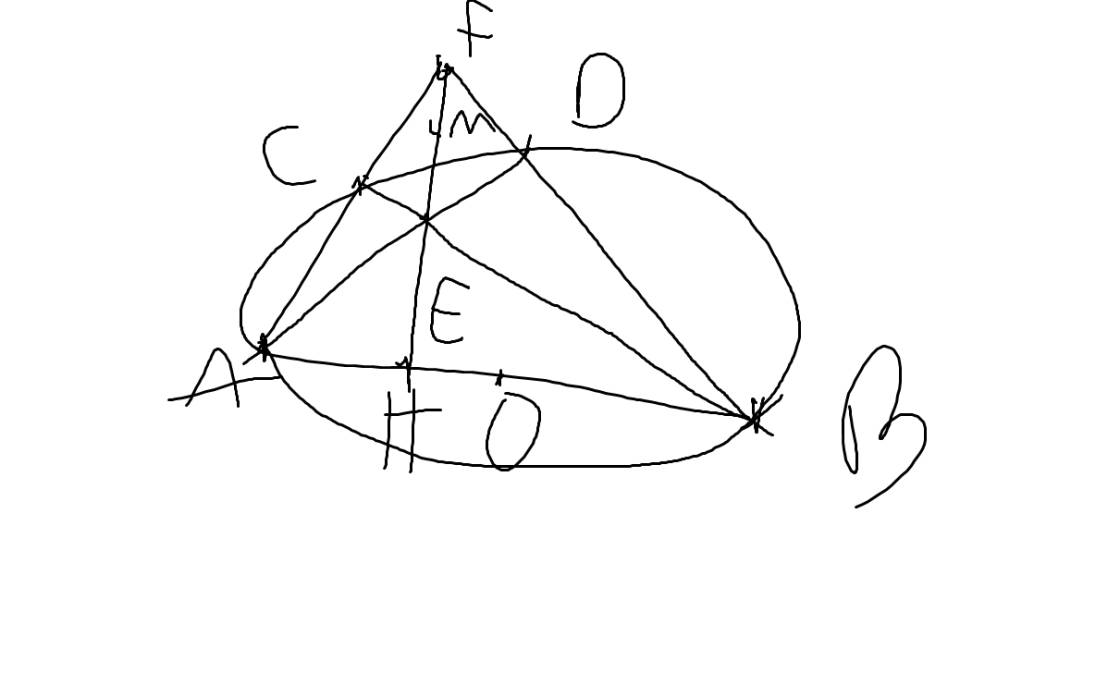
a: góc AEB=góc AHB=90 độ
=>ABHE nôi tiếp
b: Gọi N là trung điểm của AB
=>AN=HN=EN=BN
MN là đường trung bình của ΔABC
=>MN//AC
HE vuông góc AC
=>HE vuông góc MN
=>MN là trung trực của HE
=>ME=MH
5 tháng 11 2023
10:
\(a+b=50^0+40^0=90^0\)
=>\(sina=cosb;sinb=cosa;tana=cotb;cota=tanb\)
=>sina=cosb
=>Chọn C
11:
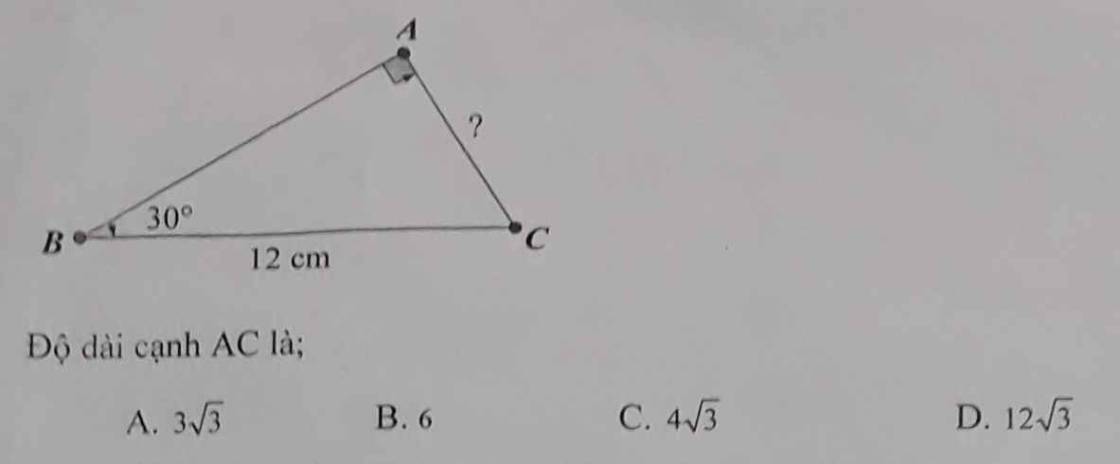
Xét ΔABC vuông tại A có \(AC=BC\cdot sinB\)
=>\(AC=12\cdot sin30=6\)
=>Chọn B
V
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm
T
1
LT
1
11 tháng 11 2023
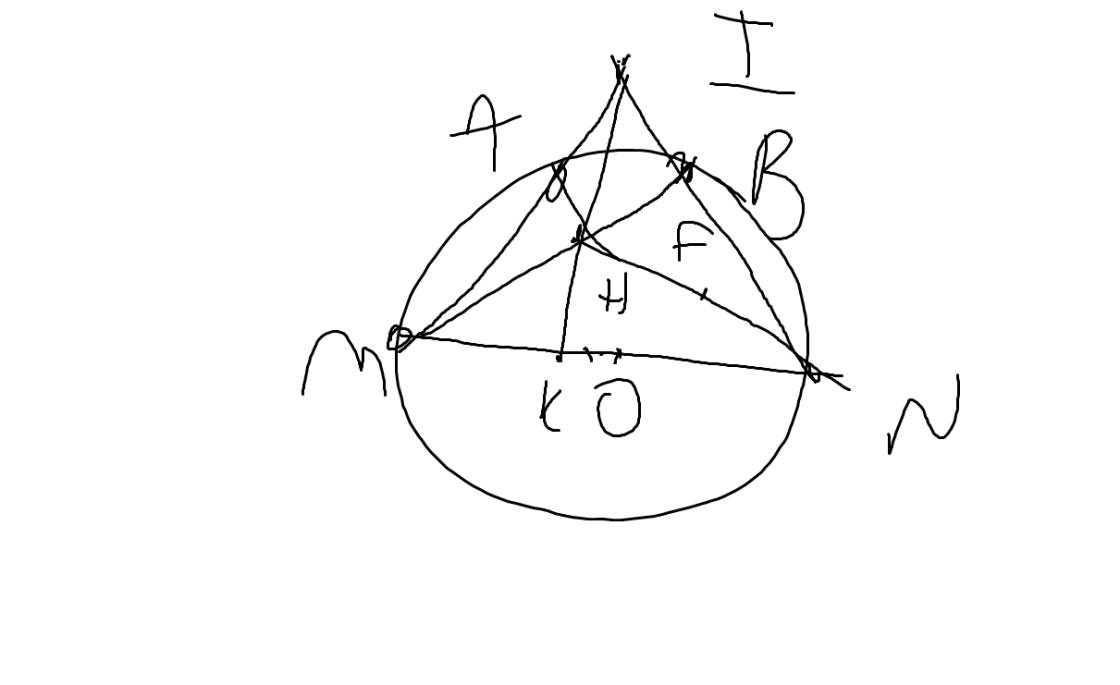
a: Xét (O) có
ΔMAN nội tiếp
MN là đường kính
Do đó: ΔMAN vuông tại A
=>NA\(\perp\)IM
Xét (O) có
ΔNBM nội tiếp
NM là đường kính
Do đó: ΔNBM vuông tại B
=>MB\(\perp\)NI
b: Xét ΔIMN có
MB,NA là đường cao
MB cắt NA tại H
Do đó: H là trực tâm
=>IH\(\perp\)MN tại K
Xét tứ giác BHKN có
\(\widehat{HBN}+\widehat{HKN}=90^0+90^0=180^0\)
=>BHKN nội tiếp đường tròn đường kính HN
tâm F là trung điểm của HN
18 tháng 8 2023
a: \(AB=\sqrt{CA^2+CB^2}=25\left(cm\right)\)
Xét ΔABC vuông tại C có sin A=BC/BA=4/5
nên góc A\(\simeq\)53 độ
=>góc B=90-53=37 độ
ΔCAB vuông tại C có CH là đường cao
nên CH*AB=CA*CB
=>CH*25=15*20=300
=>CH=12(cm)
b: ΔHCA vuông tại H có HE là đường cao
nên CE*CA=CH^2
ΔCHB vuông tại H có FH là đường cao
nên CF*CB=CH^2
=>CE*CA=CF*CB
12 tháng 10 2021
Câu 2:
Ta có: \(\sqrt{x^2-4x+4}=x-1\)
\(\Leftrightarrow2-x=x-1\left(x< 2\right)\)
\(\Leftrightarrow-2x=-3\)
hay \(x=\dfrac{3}{2}\left(tm\right)\)
LT
1
11 tháng 11 2023
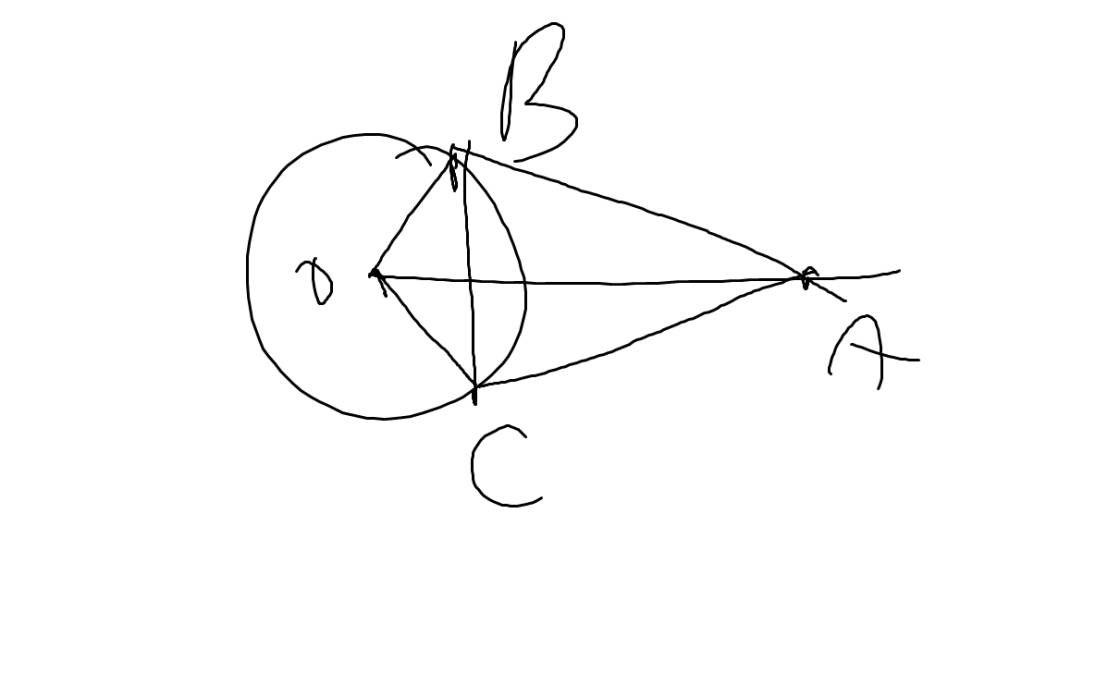
a: AB và AC là hai tiếp tuyến cắt nhau tại A
b: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>OBAC là tứ giác nội tiếp
=>O,B,A,C cùng thuộc 1 đường tròn