LT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 12 2023
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA tại C
=>CB\(\perp\)AF tại C
Xét tứ giác BHCF có \(\widehat{BHF}=\widehat{BCF}=90^0\)
nên BHCF là tứ giác nội tiếp
=>B,H,C,F cùng thuộc một đường tròn
NP
1
5 tháng 4 2023
a: góc AEB=góc AHB=90 độ
=>ABHE nôi tiếp
b: Gọi N là trung điểm của AB
=>AN=HN=EN=BN
MN là đường trung bình của ΔABC
=>MN//AC
HE vuông góc AC
=>HE vuông góc MN
=>MN là trung trực của HE
=>ME=MH
HA
0
12 tháng 12 2021
khi bài toán bắt ta chứng minh một hình gì đó mà thiếu một ta hay một đường thẳng...
8 tháng 12 2021
\(M=\left(\dfrac{a-1}{2\sqrt{a}}\right)^2\cdot\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\\ M=\dfrac{\left(a-1\right)^2}{4a}\cdot\dfrac{-4\sqrt{a}}{a-1}=\dfrac{1-a}{\sqrt{a}}\)
8 tháng 12 2021
anh có thể ghi thêm các bước trước khi ra đc mấy cái này ko ạ tại rút gọn quá e ch hỉu ạ e c.ơn
NL
3
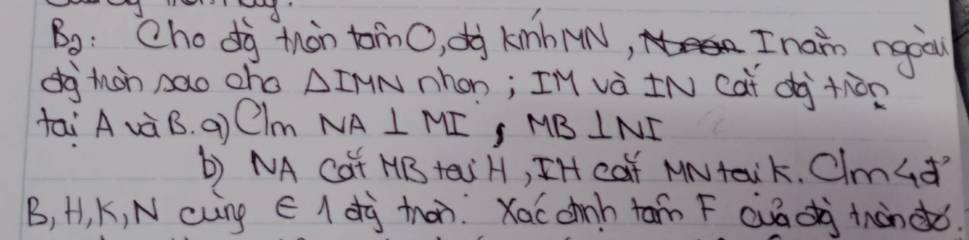
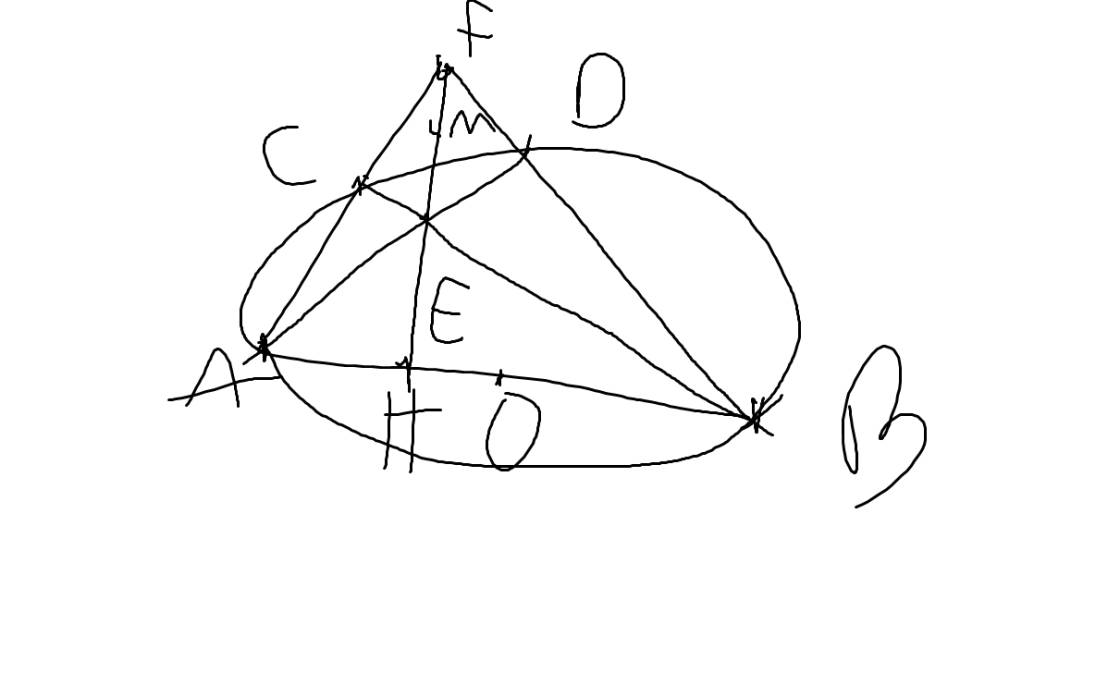
a: Xét (O) có
ΔMAN nội tiếp
MN là đường kính
Do đó: ΔMAN vuông tại A
=>NA\(\perp\)IM
Xét (O) có
ΔNBM nội tiếp
NM là đường kính
Do đó: ΔNBM vuông tại B
=>MB\(\perp\)NI
b: Xét ΔIMN có
MB,NA là đường cao
MB cắt NA tại H
Do đó: H là trực tâm
=>IH\(\perp\)MN tại K
Xét tứ giác BHKN có
\(\widehat{HBN}+\widehat{HKN}=90^0+90^0=180^0\)
=>BHKN nội tiếp đường tròn đường kính HN
tâm F là trung điểm của HN