K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 12 2023
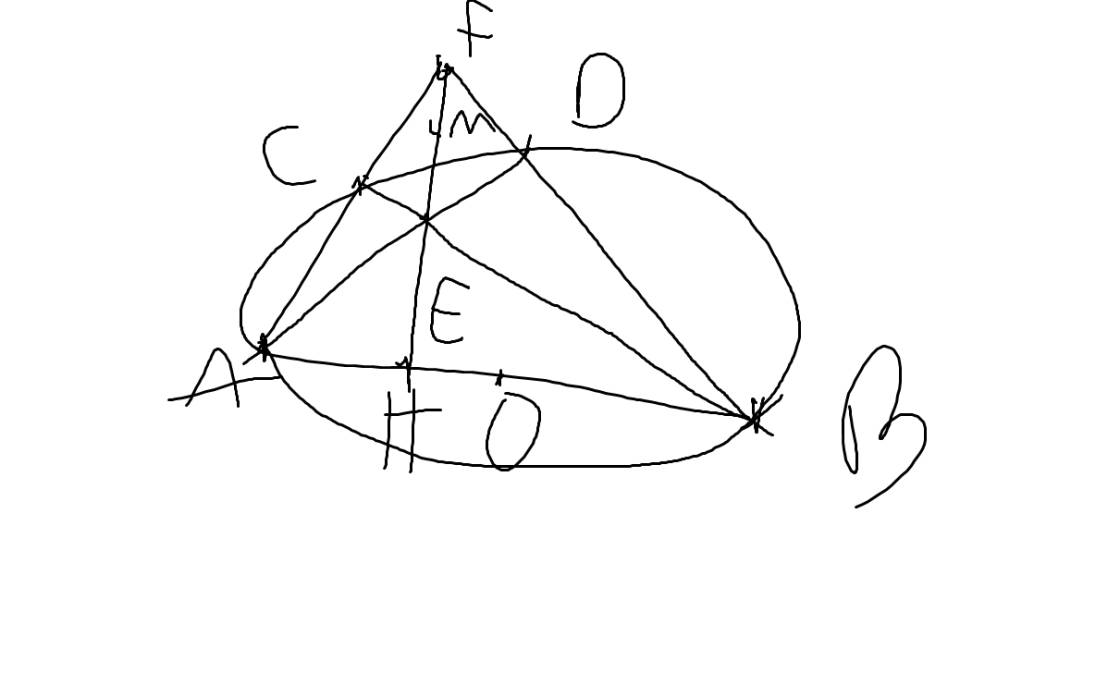
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA tại C
=>CB\(\perp\)AF tại C
Xét tứ giác BHCF có \(\widehat{BHF}=\widehat{BCF}=90^0\)
nên BHCF là tứ giác nội tiếp
=>B,H,C,F cùng thuộc một đường tròn
15 tháng 10 2021
Xét ΔAMO vuông tại M có
\(OA^2=AM^2+OM^2\)
\(\Leftrightarrow AM=12\left(cm\right)\)
hay AB=24(cm)
NC
4
1 tháng 11 2021
\(11,\\ a,=4\cdot5+14:7=20+2=22\\ b,=3\sqrt{2}-12\sqrt{2}+5\sqrt{2}=-4\sqrt{2}\\ c,=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)}=\dfrac{6}{7}\\ 12,\\ a,P=\dfrac{\sqrt{x}+3+\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}\\ P=\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}=\dfrac{2}{\sqrt{x}+3}\\ b,P=\dfrac{1}{2}\Leftrightarrow\sqrt{x}+3=4\Leftrightarrow x=1\left(tm\right)\)
1 tháng 11 2021
a: \(=4\cdot5+14:7=20+2=22\)
b: \(=3\sqrt{2}-8\sqrt{2}+5\sqrt{2}=0\)
LT
1
11 tháng 11 2023
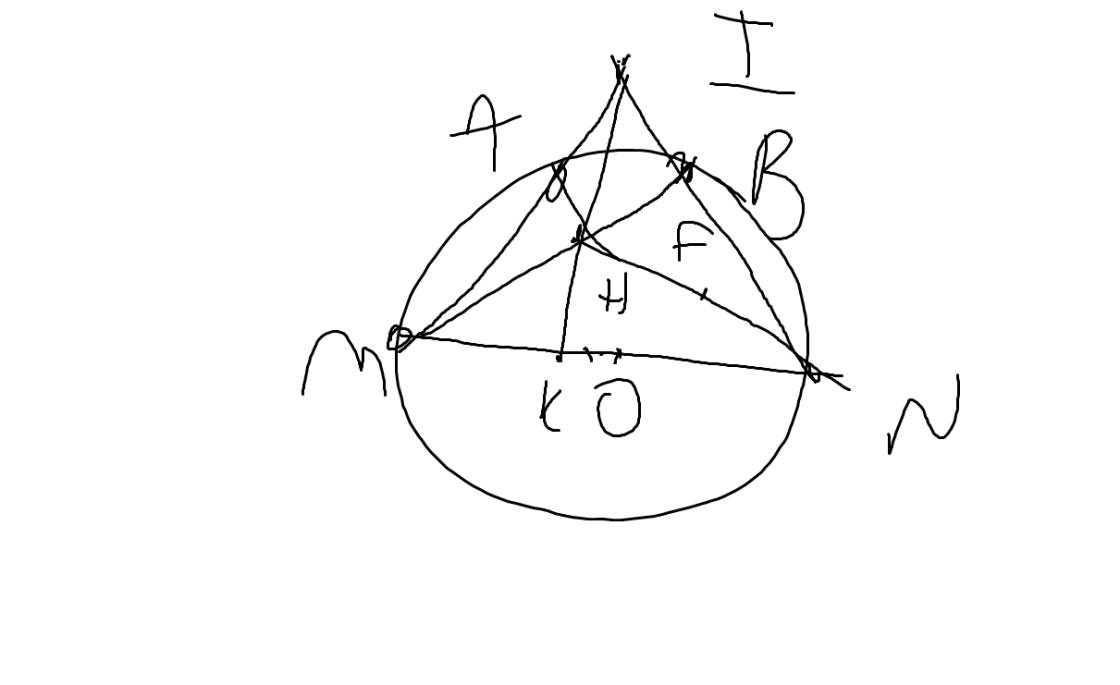
a: Xét (O) có
ΔMAN nội tiếp
MN là đường kính
Do đó: ΔMAN vuông tại A
=>NA\(\perp\)IM
Xét (O) có
ΔNBM nội tiếp
NM là đường kính
Do đó: ΔNBM vuông tại B
=>MB\(\perp\)NI
b: Xét ΔIMN có
MB,NA là đường cao
MB cắt NA tại H
Do đó: H là trực tâm
=>IH\(\perp\)MN tại K
Xét tứ giác BHKN có
\(\widehat{HBN}+\widehat{HKN}=90^0+90^0=180^0\)
=>BHKN nội tiếp đường tròn đường kính HN
tâm F là trung điểm của HN
6 tháng 7 2023
1.4:
a: CH=16^2/24=256/24=32/3
BC=24+32/3=104/3
AC=căn 32/3*104/3=16/3*căn 13
b: BC=12^2/6=24
AC=căn 24^2-12^2=12*căn 3
CH=24-6=18
12 tháng 10 2021
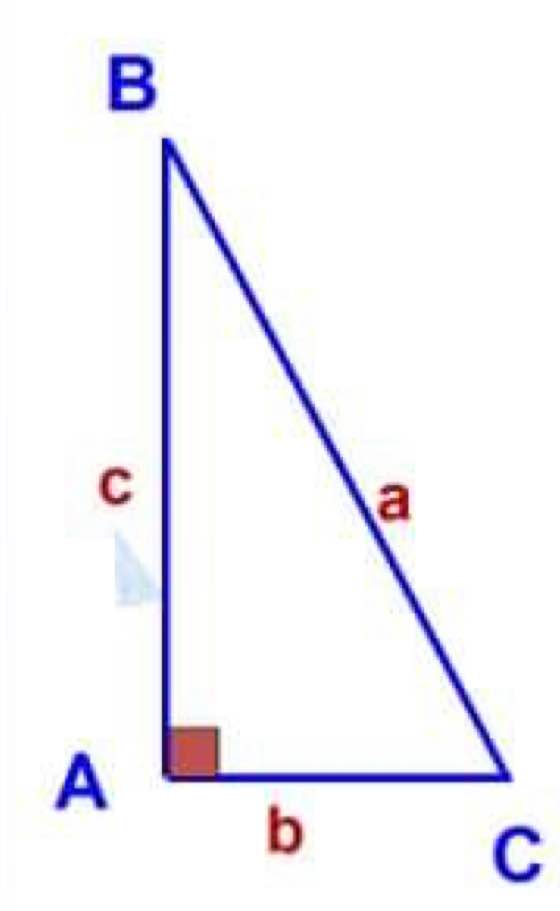
a: \(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}\)
NP
1
5 tháng 4 2023
a: góc AEB=góc AHB=90 độ
=>ABHE nôi tiếp
b: Gọi N là trung điểm của AB
=>AN=HN=EN=BN
MN là đường trung bình của ΔABC
=>MN//AC
HE vuông góc AC
=>HE vuông góc MN
=>MN là trung trực của HE
=>ME=MH
29 tháng 3 2021
a) Xét ΔOAB có OA=OB=AB(=R)
nên ΔOAB đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{AOB}=60^0\)
\(\Leftrightarrow sđ\stackrel\frown{AB}=60^0\)