Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔAMO vuông tại M có
\(OA^2=AM^2+OM^2\)
\(\Leftrightarrow AM=12\left(cm\right)\)
hay AB=24(cm)

a) Xét (O) có
\(\widehat{BAD}\) là góc nội tiếp chắn \(\stackrel\frown{BD}\)
\(\widehat{BCD}\) là góc nội tiếp chắn \(\stackrel\frown{BD}\)
Do đó: \(\widehat{BAD}=\widehat{BCD}\)(Hệ quả góc nội tiếp)
hay \(\widehat{IAD}=\widehat{ICB}\)
Xét ΔIAD và ΔICB có
\(\widehat{IAD}=\widehat{ICB}\)(cmt)
\(\widehat{AID}=\widehat{CIB}\)(hai góc đối đỉnh)
Do đó: ΔIAD\(\sim\)ΔICB(g-g)
Suy ra: \(\dfrac{IA}{IC}=\dfrac{ID}{IB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(IA\cdot IB=IC\cdot ID\)(đpcm)

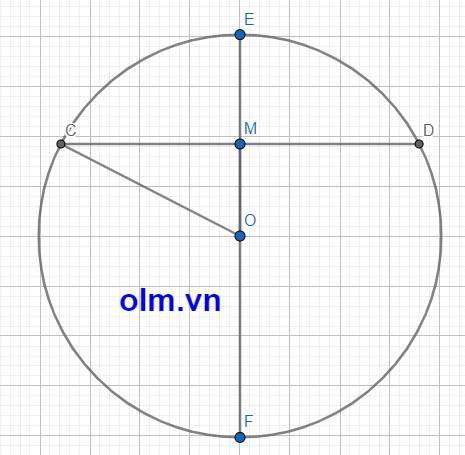
Dây dài nhất đi qua M là đường kính đi qua M của đường tròn.
Dây ngắn nhất đi qua M là dây đi qua M và vuông góc với OM tại M
Dộ dài dây dài nhất đi qua M là: 13 x 2 = 26 (cm)
Độ dài của dây ngắn nhất đi qua M là: CD = CM x 2
CD = 2x \(\sqrt{CO^2-OM^2}\)
CD = 2x\(\sqrt{13^2-5^2}\)
CD = 24 (cm)
Từ những lập luận trên ta có những dây đi qua M có độ dài là số tự nhiên là những dây có độ dài lần lượt là 24cm; 25cm; 26cm
Vậy có 3 dây đi qua M và có độ dài là số tự nhiên.

Xét (O) có
OH là một phần đường kính
MN là dây
OH⊥MN tại H
Do đó: H là trung điểm của MN
=>HM=HN=MN/2=3(cm)
Xét ΔOHM vuông tại H có
\(OM^2=OH^2+HM^2\)
hay OH=4cm
Xét ΔAMO vuông tại M có
\(OA^2=AM^2+OM^2\)
\(\Leftrightarrow AM=12\left(cm\right)\)
hay AB=24(cm)