Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d.
Ta có: \(AB=AC\) (t/c hai tiếp tuyến cắt nhau)
\(OB=OC=R\)
\(\Rightarrow OA\) là trung trực BC hay OA vuông góc BC tại I
Xét hai tam giác vuông AIB và ABO có:
\(\left\{{}\begin{matrix}\widehat{AIB}=\widehat{ABO}=90^0\\\widehat{BAI}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta AIB\sim\Delta ABO\left(g.g\right)\)
\(\Rightarrow\dfrac{AI}{AB}=\dfrac{AB}{AO}\Rightarrow AI.AO=AB^2\)
Theo c/m câu c có \(AB^2=AE.AF\)
\(\Rightarrow AI.AO=AE.AF\)
e.
Từ đẳng thức trên ta suy ra: \(\dfrac{AI}{AF}=\dfrac{AE}{AO}\)
Xét hai tam giác AIE và AFO có:
\(\left\{{}\begin{matrix}\dfrac{AI}{AF}=\dfrac{AE}{AO}\left(cmt\right)\\\widehat{OAF}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta AIE\sim\Delta AFO\left(c.g.c\right)\)
\(\Rightarrow\widehat{AFO}=\widehat{AIE}\)
Mà \(\widehat{AIE}+\widehat{OIE}=180^0\) (kề bù)
\(\Rightarrow\widehat{AFO}+\widehat{OIE}=180^0\)
\(\Rightarrow\) Tứ giác FOIE nội tiếp
a.
Do AB là tiếp tuyến của (O) \(\Rightarrow AB\perp OB\Rightarrow\widehat{ABO}=90^0\)
\(\Rightarrow\) 3 điểm A, B, O thuộc đường tròn đường kính OA (1)
Tương tự AC là tiếp tuyến của (O) nên 3 điểm A, C, O thuộc đường tròn đường kính OA
\(\Rightarrow\) 4 điểm A, B, C, O thuộc đường tròn đường kính OA hay tứ giác ABOC nội tiếp
b.
Do M là trung điểm EF \(\Rightarrow OM\perp EF\Rightarrow\widehat{OMA}=90^0\)
\(\Rightarrow\) 3 điểm A, M, O thuộc đường tròn đường kính OA (2)
(1);(2) \(\Rightarrow\) 4 điểm A, B, M, O thuộc đường tròn đường kính OA
Hay tứ giác ABMO nội tiếp
c.
Xét hai tam giác ABE và AFB có:
\(\left\{{}\begin{matrix}\widehat{EAB}\text{ chung}\\\widehat{ABE}=\widehat{AFB}\left(\text{cùng chắn BE}\right)\end{matrix}\right.\) \(\Rightarrow\Delta ABE\sim\Delta AFB\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AF}=\dfrac{AE}{AB}\) \(\Rightarrow AB^2=AE.AF\)


b: Vì (d)//(d') nên a=2
Vậy: y=2x+b
Thay x=1 và y=-2 vào (d), ta được:
b+2=-2
hay b=-4

thì mình lấy giả thiết của định lí thuận làm kết luận, kết luận của định lí thuận làm giả thiết

\(11,\\ a,=4\cdot5+14:7=20+2=22\\ b,=3\sqrt{2}-12\sqrt{2}+5\sqrt{2}=-4\sqrt{2}\\ c,=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)}=\dfrac{6}{7}\\ 12,\\ a,P=\dfrac{\sqrt{x}+3+\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}\\ P=\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}=\dfrac{2}{\sqrt{x}+3}\\ b,P=\dfrac{1}{2}\Leftrightarrow\sqrt{x}+3=4\Leftrightarrow x=1\left(tm\right)\)
a: \(=4\cdot5+14:7=20+2=22\)
b: \(=3\sqrt{2}-8\sqrt{2}+5\sqrt{2}=0\)

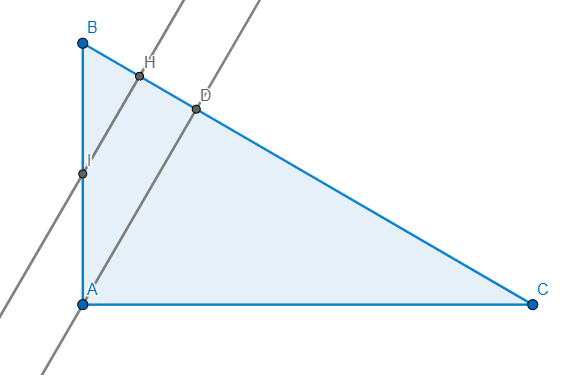
Kẻ đường cao AD \(\Rightarrow IH\parallel AD(\bot BC)\)
mà I là trung điểm AB nên H là trung điểm BD
Ta có: \(HC^2-HB^2=\left(HC-HB\right)\left(HC+HB\right)=\left(HC-DH\right).BC\)
\(=CD.BC\)
tam giác ABC vuông tại A có đường cao AD nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CD.BC\Rightarrow\) đpcm




khi bài toán bắt ta chứng minh một hình gì đó mà thiếu một ta hay một đường thẳng...
bn giải thik rõ hơn đc k ạ !!!