Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Để ý rằng với mỗi hcn tạo ra sẽ có 2 đường chéo đi qua tâm O.
Cứ 2 cặp đường chéo như vậy sẽ tương ứng với một hình chữ nhật. Mà có $10$ đường chéo đi qua tâm nên có số hình chữ nhật được tạo thành là:
$C^2_10=45$

Số tam giác có các đỉnh là 3 trong 2n điểm A1;A2;…;A2n là: ![]()
Ta thấy ứng với hai đường chéo đi qua tâm O của đa giác A1A2…A2n cho tương ứng một hình chữ nhật có 4 đỉnh là 4 điểm trong 2n điểm A1;A2;…;A2n và ngược lại mỗi hình chữ nhật như vậy sẽ cho tương ứng hai đường chéo đi qua tâm O của đa giác.
Mà số đường chéo đi qua tâm của đa giác là n nên số hình chữ nhật có đỉnh là 4 trong 2n điểm bằng ![]()
Theo giả thiết: ![]()
⇒n=8.
Chọn C

Đáp án B
Đa giác đều 2n đỉnh có n đường chéo qua tâm. Cứ 2 đường chéo qua tâm tương ứng với 1 hình chữ nhật ⇒ C n 2 = 45 ⇔ n = 10

Đáp án C
Chọn ngẫu nhiên 4 đỉnh của đa giác có C 20 4 = 4845 c á c h
Đa giác đều 20 đỉnh có 10 đường chéo đi qua tâm đường tròn ngoại tiếp đa giác
Cứ 2 đường chéo bất kì là 2 đường chéo cuiả 1 hình chữ nhật
Do đó số hình chứ nhật là C 20 2 = 45
Vậy xác suất cần tìm là
P = 45 4845 = 3 323

Đáp án A.
Có 10 đường kính của đường tròn được nối bởi 2 đỉnh của đa giác đều
Một hình chữ nhật có 4 đỉnh là đỉnh của đa giác được tạo bởi 2 đường kính nói trên
Số cách chọn 4 đỉnh của đa giác là C 20 4
Số cách chọn 4 đỉnh của hình chữ nhật là C 20 2
Vậy xác suất cần tính là P = C 10 2 C 20 4 = 3 323

Đáp án A
Ta có số cách chọn 4 đỉnh: ![]()
Hình hai mươi cạnh đều có 10 đường chéo đi qua tâm và chúng đều bằng nhau
Cứ hai đường chéo gộp lại ta được hai đường chéo của một hình chữ nhật
Vậy có tất cả ![]() hình chữ nhật thỏa mãn 4 đỉnh là 4 trong 20 đỉnh của hình cho
hình chữ nhật thỏa mãn 4 đỉnh là 4 trong 20 đỉnh của hình cho
Kết luận:
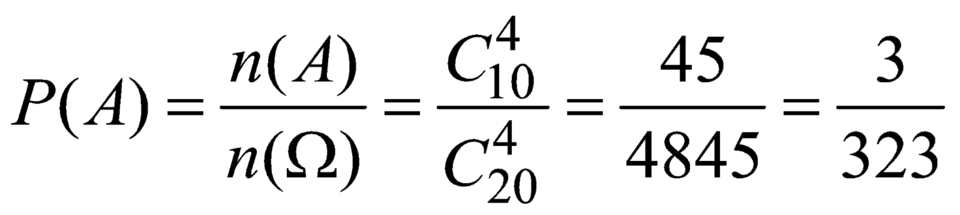

Đáp án A
Có 10 đường kính của đường tròn được nối bởi 2 đỉnh của đa giác đều. Một hình chữ nhật có 4 đỉnh là đỉnh của một đa giác được tạo bởi 2 đường kính nói trên. Số cach chọn 4 đỉnh của đa giác là: ![]() .
.
Xác suất cần tìm là:
![]()


Gọi (O) là đường tròn ngoại tiếp đa giác, do đa giác có số đỉnh là số chẳn nên đường nối một đỉnh tùy ý với tâm O sẽ đi qua một đỉnh khác (ta gọi là 2 điểm xuyên tâm đối)
do đa giác có n đỉnh nên có \(\frac{n}{2}\) cặp điểm xuyên tâm đối (hay có \(\frac{n}{2}\) đường chéo đi qua tâm O)
với mỗi hai đường chéo qua tâm O ta được 1 hình chữ nhật
vì có 12 hình chữ nhật và có \(\frac{n}{2}\) đường chéo nên : \(C_{\frac{n}{2}}^2=15\left(dk:n\ge4\right)\)\(\Leftrightarrow\frac{\left(\frac{n}{2}\right)!}{2!.\left(\frac{n}{2}-2\right)!}=15\) \(\Leftrightarrow\frac{\frac{n}{2}.\left(\frac{n}{2}-1\right).\left(\frac{n}{2}-2\right)!}{2.\left(\frac{n}{2}-2\right)!}=15\) \(\Leftrightarrow\frac{\frac{n}{2}.\left(\frac{n}{2}-1\right)}{2}=15\Leftrightarrow\frac{n}{2}.\left(\frac{n}{2}-1\right)=30\Leftrightarrow n^2-2n=120\Leftrightarrow\left[\begin{array}{nghiempt}n=12\\n=-10\left(loai\right)\end{array}\right.\)
Vậy \(n=12\) thỏa mãn