

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Không gian mẫu \(\Omega\) là tập hợp tất cả các cách chọn ngẫu nhiên 4 đỉnh trong 12 đỉnh
Ta có \(n\left(\Omega\right)=C_{12}^4=495\)
Gọi A là biến cố : 4 đỉnh được chọn tạo thành một hình chữ nhật"
Gọi đường chéo của đa giác đều \(A_1A_2A_3...A_{12}\) đi qua tâm đường tròn (O) là đường chéo lớn thì đa giác đã cho có 6 đường chéo lớn.
Mỗi hình chữ nhật có các đỉnh là 4 đỉnh trong 12 điểm \(A_1,A_2,A_3,...A_{12}\) có các đường chéo là 2 đường chéo lớn. Ngược lại, mỗi cặp đường chéo lớn có các đầu mút là 4 đỉnh của một hình chữ nhâtk.
Do đó, số hình chữ nhật được tạo thành là : \(n\left(A\right)=C_6^2=15\)
Vậy xác suất cần tính là \(P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega\right)}=\frac{15}{495}=\frac{1}{33}\)

Đáp án A
Có 10 đường kính của đường tròn được nối bởi 2 đỉnh của đa giác đều. Một hình chữ nhật có 4 đỉnh là đỉnh của một đa giác được tạo bởi 2 đường kính nói trên. Số cach chọn 4 đỉnh của đa giác là: ![]() .
.
Xác suất cần tìm là:
![]()

Đáp án A.
Có 10 đường kính của đường tròn được nối bởi 2 đỉnh của đa giác đều
Một hình chữ nhật có 4 đỉnh là đỉnh của đa giác được tạo bởi 2 đường kính nói trên
Số cách chọn 4 đỉnh của đa giác là C 20 4
Số cách chọn 4 đỉnh của hình chữ nhật là C 20 2
Vậy xác suất cần tính là P = C 10 2 C 20 4 = 3 323

Đáp án A
Ta có số cách chọn 4 đỉnh: ![]()
Hình hai mươi cạnh đều có 10 đường chéo đi qua tâm và chúng đều bằng nhau
Cứ hai đường chéo gộp lại ta được hai đường chéo của một hình chữ nhật
Vậy có tất cả ![]() hình chữ nhật thỏa mãn 4 đỉnh là 4 trong 20 đỉnh của hình cho
hình chữ nhật thỏa mãn 4 đỉnh là 4 trong 20 đỉnh của hình cho
Kết luận:
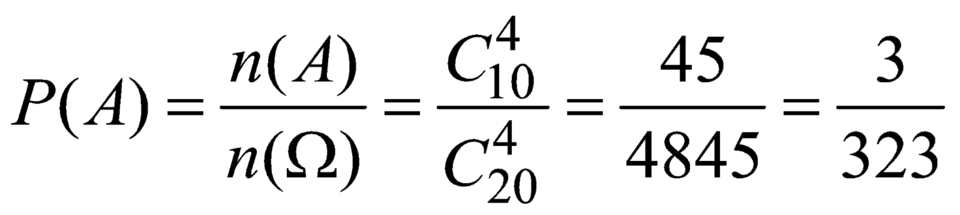

Đáp án C
Chọn ngẫu nhiên 4 đỉnh của đa giác có C 20 4 = 4845 c á c h
Đa giác đều 20 đỉnh có 10 đường chéo đi qua tâm đường tròn ngoại tiếp đa giác
Cứ 2 đường chéo bất kì là 2 đường chéo cuiả 1 hình chữ nhật
Do đó số hình chứ nhật là C 20 2 = 45
Vậy xác suất cần tìm là
P = 45 4845 = 3 323

2 : cho ab=cd(a,b,c,d≠0)ab=cd(a,b,c,d≠0) và đôi 1 khác nhau, khác đôi nhau
Chứng minh :
a) C1: Đặt \(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow\left\{{}\begin{matrix}a=kb\\c=kd\end{matrix}\right.\)
\(\frac{a-b}{a+b}=\frac{kb-b}{kb+b}=\frac{b\left(k-1\right)}{b\left(k+1\right)}=\frac{k-1}{k+1}\)
\(\frac{c-d}{c+d}=\frac{kd-d}{kd+d}=\frac{d\left(k-1\right)}{d\left(k+1\right)}\frac{k-1}{k+1}\)
Bài 1:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{\dfrac{3}{2}}=\dfrac{z}{\dfrac{4}{3}}=\dfrac{x-y}{2-\dfrac{3}{2}}=\dfrac{15}{\dfrac{1}{2}}=30\)
Do đó: x=60; y=45; z=40
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
Do đó: x=20; y=30; z=42

SỐ tam giác tạo được từ 3 đỉnh là \(C^3_{12}\)
Số tam giác có 3 đỉnh là 3 đỉnh của đa giác và 2 cạnh là cạnh của đa giác: cứ 3 đỉnh liên tiếp cho 1 tam giác thỏa mãn
=>Có 12 tam giác
Số tam giác có 3 đỉnh là đỉnh của đa giác và 1 cạnh là cạnh của đa giác
=>CÓ 8*12=96 tam giác
=>\(P=\dfrac{C^3_{12}-12-12\cdot8}{C^3_{12}}\)

Đáp án C
+) Số tam giác được tạo từ 3 đỉnh trong 12 đỉnh: C 12 3
+) Số tam giác có 3 đỉnh là đỉnh của đa giác và 2 cạnh là cạnh của đa giác: cứ 3 đỉnh liên tiếp cho 1 tam giác thỏa mãn đề bài, nên có 12 tam giác
+) Số tam giác có 3 đỉnh là đỉnh của đa giác và 1 cạnh là cạnh của đa giác: cứ 1 cạnh, trừ đi 2 đỉnh kể, còn 8 đỉnh, với 2 đỉnh đầu mút của cạnh đó cho 1 tam giác thỏa mãn đề bài, nên có 8.12 tam giác
Vậy số tam giác có 3 đỉnh là đỉnh của đa giác và không có cạnh nào là cạnh của đa giác là C 12 3 - 12 - 12 . 8
Vậy kết quả là C 12 3 - 12 - 12 . 8 C 12 3