Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số tam giác là \(C_{2n}^3\). Một đa giác đều 2n đỉnh thì có n đường chéo xuyên tâm. Cứ 2 đường chéo xuyên tâm thì có một hình chữ nhật theo yêu cầu. Vậy số hình chữ nhật là \(C_n^2\).
Theo bài ta có phương trình :
\(C_{2n}^3=20C_n^2,\left(n\ge2\right)\)
\(\Leftrightarrow\frac{\left(2n\right)!}{\left(2n-3\right)!3!}=20\frac{n!}{\left(n-2\right)!2!}\)
\(\Leftrightarrow\frac{\left(2n-2\right)\left(2n-1\right)2n}{3}=20\left(n-1\right)n\)
\(\Leftrightarrow2\left(n-1\right)\left(2n-1\right)2n=60\left(n-1\right)n\)
\(\Leftrightarrow2n-1=15\), (do \(n\ge2\))
\(\Leftrightarrow n=18\)
Vậy đa giác đều có 16 cạnh, (thập lục giác đều)

Chọn B
· Bổ đề: Trong mặt phẳng cho hai tia Ox và Oy vuông góc với nhau tại gốc O. Trên tia Ox lấy 10 điểm A 1 , A 2 , . . . , A 10 và trên tia Oy lấy 10 điểm B 1 , B 2 , . . . . , B 10 thỏa mãn O A 1 = A 1 A 2 = . . . = A 9 A 10 = O B 1 = B 1 B 2 = . . . . = B 9 B 10 = 1 (đvd).
Tìm số tam giác có 2 đỉnh nằm trong 10 điểm ![]() 1 đỉnh nằm trong 10 điểm
B
1
,
B
2
,
.
.
.
.
,
B
10
sao cho tam giác chọn được có đường tròn ngoại tiếp, tiếp xúc với một trong hai trục Ox hoặc Oy?
1 đỉnh nằm trong 10 điểm
B
1
,
B
2
,
.
.
.
.
,
B
10
sao cho tam giác chọn được có đường tròn ngoại tiếp, tiếp xúc với một trong hai trục Ox hoặc Oy?
Giải: Gọi ![]() là 3 đỉnh của tam giác thỏa yêu cầu bài toán với
là 3 đỉnh của tam giác thỏa yêu cầu bài toán với ![]()
Ta có ![]()
Do đường tròn luôn cắt Ox tại ![]() phân biệt nên đường tròn chỉ có thể tiếp xúc với Oy tại
B
p
ta có phương tích
phân biệt nên đường tròn chỉ có thể tiếp xúc với Oy tại
B
p
ta có phương tích
![]()
Do ![]() nên dễ thấy
nên dễ thấy ![]()
hay nói cách khác bộ ba (m,n,p) ![]()
Vậy có 4 tam giác thỏa mãn yêu cầu bổ đề.
· Bài toán: Không gian mẫu ![]()
Gọi A là biến cố chọn được tam giác có đường tròn ngoại tiếp tiếp xúc với một trong hai trục Ox hoặc Oy. Theo bổ đề ta chọn được 4 tam giác có 2 đỉnh thuộc tia Ox, 1 đỉnh thuộc tia Oy; tương tự có 4 tam giác có 1 đỉnh thuộc tia Oy, đỉnh thuộc tia . Suy ra, n(A) = 8
Xác suất biến cố A là 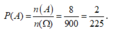

Số tam giác: \(C_{2n}^3=\frac{\left(2n\right)!}{\left(2n-3\right)!.6}=\frac{n\left(2n-1\right)\left(2n-2\right)}{3}\)
Cứ hai đường chéo qua tâm của đa giác đều sẽ đóng vai trò hai đường chéo của hình chữ nhật
Đa giác có \(n\) đường chéo qua tâm \(\Rightarrow C_n^2=\frac{n\left(n-1\right)}{2}\) hình chữ nhật
Ta có pt:
\(\frac{n\left(2n-1\right)\left(2n-2\right)}{3}=10n\left(n-1\right)\)
\(\Leftrightarrow n\left(n-1\right)\left(n-8\right)=0\Rightarrow n=8\)

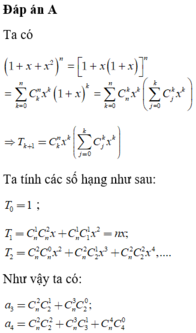
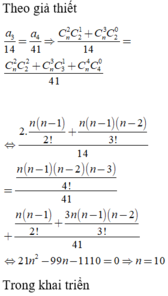
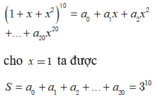


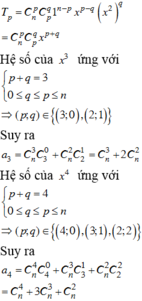
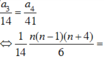
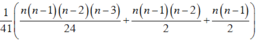
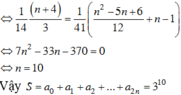

Số tam giác có các đỉnh là 3 trong 2n điểm A1;A2;…;A2n là: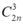
Ta thấy ứng với hai đường chéo đi qua tâm O của đa giác A1A2…A2n cho tương ứng một hình chữ nhật có 4 đỉnh là 4 điểm trong 2n điểm A1;A2;…;A2n và ngược lại mỗi hình chữ nhật như vậy sẽ cho tương ứng hai đường chéo đi qua tâm O của đa giác.
Mà số đường chéo đi qua tâm của đa giác là n nên số hình chữ nhật có đỉnh là 4 trong 2n điểm bằng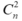
Theo giả thiết: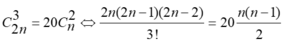
⇒n=8.
Chọn C