Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có thể đưa về hàm số:
\(AB=2\Rightarrow MB=\sqrt{AB^2-MA^2}=\sqrt{4-MA^2}\)
Đặt \(MA=t\) với \(0\le t\le2\) \(\Rightarrow MB=\sqrt{4-t^2}\)
\(P=MA+2MB=f\left(t\right)=t+2\sqrt{4-t^2}\)
Xét hàm \(f\left(t\right)\) trên \(\left[0;2\right]\)
\(f'\left(t\right)=1-\dfrac{2t}{\sqrt{4-t^2}}=0\Rightarrow2t=\sqrt{4-t^2}\Rightarrow5t^2=4\Rightarrow t=\dfrac{2}{\sqrt{5}}\)
\(f\left(0\right)=4\) ; \(f\left(2\right)=2\) ; \(f\left(\dfrac{2}{\sqrt{5}}\right)=2\sqrt{5}\)
\(\Rightarrow f\left(t\right)_{max}=2\sqrt{5}\Rightarrow P_{max}=2\sqrt{5}\)

\(4=2^x+2^y\ge2\sqrt{2^{x+y}}\Rightarrow2^{x+y}\le4\Rightarrow x+y\le2\)
\(\Rightarrow xy\le1\)
\(P=4x^2y^2+2x^3+2y^3+10xy\)
\(P=4x^2y^2+10xy+2\left(x+y\right)\left[\left(x+y\right)^2-3xy\right]\)
\(P\le4x^2y^2+10xy+4\left(4-3xy\right)=4x^2y^2-2xy+16\)
Đặt \(xy=t\Rightarrow0< t\le1\)
Xét hàm \(f\left(t\right)=4t^2-2t+16\) trên \((0;1]\)
\(\Rightarrow...\)

\(\Leftrightarrow2y^3-6y^2+7y-3=-2x\sqrt{1-x}+2\sqrt{1-x}+\sqrt{1-x}\)
\(\Leftrightarrow2\left(y^3-3y^2+3y+1\right)+y-1=2\left(1-x\right)\sqrt{1-x}+\sqrt{1-x}\)
\(\Leftrightarrow2\left(y-1\right)^3+y-1=2\left(\sqrt{1-x}\right)^3+\sqrt{1-x}\) (1)
Xét hàm \(f\left(t\right)=2t^3+t\)
\(f'\left(t\right)=6t^2+1>0\Rightarrow f\left(t\right)\) đồng biến
Nên (1) tương đương: \(y-1=\sqrt{1-x}\Rightarrow y=1+\sqrt{1-x}\)
\(\Rightarrow P=x+2\sqrt{1-x}+2=-\left(1-x-2\sqrt{1-x}+1\right)+4=-\left(\sqrt{1-x}-1\right)^2+4\le4\)
⇒ P = x + 2 √ 1 − x + 2
= − ( 1 − x − 2 √ 1 − x + 1 ) + 4
= − ( √ 1 − x − 1 ) 2 + 4 ≤ 4
Cho xin một like đi các dân chơi à.


Đặt \(\left(\dfrac{x}{6};\dfrac{y}{3};\dfrac{z}{2}\right)=\left(a;b;c\right)\Rightarrow2^{6a}+4^{3b}+8^{2c}=4\)
\(\Leftrightarrow64^a+64^b+64^c=4\)
Áp dụng BĐT Cô-si:
\(4=64^a+64^b+64^c\ge3\sqrt[3]{64^{a+b+c}}\Rightarrow64^{a+b+c}\le\dfrac{64}{27}\)
\(\Rightarrow a+b+c\le log_{64}\left(\dfrac{64}{27}\right)\Rightarrow M=log_{64}\left(\dfrac{64}{27}\right)\)
Lại có: \(x;y;z\ge0\Rightarrow a;b;c\ge0\)
\(\Rightarrow\left\{{}\begin{matrix}64^a\ge1\\64^b\ge1\\64^c\ge1\end{matrix}\right.\) \(\Rightarrow\left(64^b-1\right)\left(64^c-1\right)\ge0\)
\(\Rightarrow64^{b+c}+1\ge64^b+64^c\) (1)
Lại có: \(b+c\ge0\Rightarrow64^{b+c}\ge1\Rightarrow\left(64^a-1\right)\left(64^{b+c}-1\right)\ge0\)
\(\Rightarrow64^{a+b+c}+1\ge64^a+64^{b+c}\) (2)
Cộng vế (1);(2) \(\Rightarrow4=64^a+64^b+64^c\le64^{a+b+c}+2\)
\(\Rightarrow64^{a+b+c}\ge2\Rightarrow a+b+c\ge log_{64}2\)
\(\Rightarrow N=log_{64}2\)
\(\Rightarrow T=2log_{64}\left(\dfrac{64}{27}\right)+6log_{64}\left(2\right)\approx1,4\)

Mọi điểm M biểu diễn z đều phải thỏa mãn 2 điều kiện: vừa thuộc đường tròn (C) vừa thuộc đường thẳng \(\Delta\) (tham số P)
Do đó, M là giao điểm của (C) và \(\Delta\)
Hay tham số P phải thỏa mãn sao cho (C) và \(\Delta\) có ít nhất 1 điểm chung
Hay hệ pt nói trên có nghiệm (thật ra chi tiết đó là thừa, chỉ cần biện luận (C) và \(\Delta\) có ít nhất 1 điểm chung \(\Rightarrow d\left(I;\Delta\right)\le R\) là đủ)

Bài này thì chia 2 vế của giả thiết cho z2 ta thu được:
\(\frac{x}{z}+2.\frac{x}{z}.\frac{y}{z}+\frac{y}{z}=4\Leftrightarrow a+2ab+b=4\)
(đặt \(a=\frac{x}{z};b=\frac{y}{z}\)).Mà ta có: \(4=a+2ab+b\le a+b+\frac{\left(a+b\right)^2}{2}\Rightarrow a+b\ge2\) Lại có:
\(P=\frac{\left(\frac{x}{z}+\frac{y}{z}\right)^2}{\left(\frac{x}{z}+\frac{y}{z}\right)^2+\left(\frac{x}{z}+\frac{y}{z}\right)}+\frac{3}{2}.\frac{1}{\left(\frac{x}{z}+\frac{y}{z}+1\right)^2}\) (chia lần lượt cả tử và mẫu của mỗi phân thức cho z2)
\(=\frac{\left(a+b\right)^2}{\left(a+b\right)^2+\left(a+b\right)}+\frac{3}{2\left(a+b+1\right)^2}\).. Tiếp tục đặt \(t=a+b\ge2\) thu được:
\(P=\frac{t}{\left(t+1\right)}+\frac{3}{2\left(t+1\right)^2}=\frac{2t\left(t+1\right)+3}{2\left(t+1\right)^2}\)\(=\frac{2t^2+2t+3}{2\left(t+1\right)^2}-\frac{5}{6}+\frac{5}{6}\)
\(=\frac{2\left(t-2\right)^2}{12\left(t+1\right)^2}+\frac{5}{6}\ge\frac{5}{6}\)
Vậy...
P/s: check xem em có tính sai chỗ nào không:v
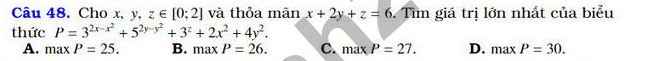


 thầy ơi giải như này được ko ạ?
thầy ơi giải như này được ko ạ? 



Do \(x;y\in\left[0;2\right]\Rightarrow\left\{{}\begin{matrix}x\left(2-x\right)\ge0\\y\left(2-y\right)\ge0\end{matrix}\right.\) \(\Rightarrow2x^2+4y^2\le4x+8y\)
\(P\le3^0+5^0+3^z+4\left(x+2y\right)=2+3^z+4\left(6-z\right)=3^z-4z+26\)
Xét hàm \(f\left(z\right)=3^z-4z+26\) trên \(\left[0;2\right]\)
\(f'\left(z\right)=3^z.ln3-4=0\Rightarrow z=log_3\left(\dfrac{4}{ln3}\right)=a\)
\(f\left(0\right)=27\) ; \(f\left(2\right)=27\); \(f\left(a\right)\approx-1,1\)
\(\Rightarrow f\left(z\right)\le27\Rightarrow maxP=27\)
(Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(0;2;2\right)\))
Ồ mà khoan, bài trước bị nhầm lẫn ở chỗ \(3^{2x-x^2}+5^{2y-y^2}\ge3^0+5^0\) mới đúng, ko để ý bị ngược dấu đoạn này
Vậy giải cách khác:
\(0\le x;y;z\le2\Rightarrow x\left(2-x\right)\ge0\Rightarrow2x-x^2\ge0\)
Lại có: \(2x-x^2=1-\left(x-1\right)^2\le1\)
\(\Rightarrow0\le2x-x^2\le1\)
Tương tự ta có: \(0\le2y-y^2\le1\)
Xét hàm: \(f\left(t\right)=3^t-2t\) trên \(\left[0;1\right]\)
\(f'\left(t\right)=3^t.ln3-2=0\Rightarrow t=log_3\left(\dfrac{2}{ln3}\right)=a\)
\(f\left(0\right)=1;\) \(f\left(1\right)=1\) ; \(f\left(a\right)\approx0,73\)
\(\Rightarrow f\left(t\right)\le1\Rightarrow3^t-2t\le1\Rightarrow3^t\le2t+1\)
\(\Rightarrow3^{2x-x^2}\le2\left(2x-x^2\right)+1\)
Hoàn toàn tương tự, ta chứng minh được:
\(5^t\le4t+1\) với \(t\in\left[0;1\right]\Rightarrow5^{2y-y^2}\le4\left(2y-y^2\right)+1\)
\(3^t\le4t+1\) với \(t\in\left[0;2\right]\Rightarrow3^z\le4z+1\)
\(\Rightarrow P\le2\left(2x-x^2\right)+4\left(2y-y^2\right)+4z+3+2x^2+4y^2=4\left(x+2y+z\right)+3=27\)
Lần này thì ko sai được rồi