Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tớ thử làm trường hợp tam giác ABC đều,còn tam giác thường chắc nhờ cô Linh Chi cứu
Tứ giác ABMC nội tiếp ( O ) nên theo định lý Ptoleme ta có \(BM\cdot AC+MC\cdot AB=BC\cdot AM\)
\(\Leftrightarrow BM+CM=AM\)
Theo BĐT Ba Con Sâu ta có:\(\frac{1}{MB}+\frac{1}{MC}\ge\frac{4}{MA}\ge\frac{4}{2R}=2R\)
Dấu "=" xảy ra tại M là điểm chính giữa cung BC

a) Ta có: \(\angle KAC=\angle KBC=90-\angle ACB=\angle HAC\)
mà \(AC\bot HK\Rightarrow\) H và K đối xứng với nhau qua AC
b) Ta có: \(\angle BEM+\angle BDM=90+90=180\Rightarrow BEMD\) nội tiếp
\(\Rightarrow\angle BED=\angle BMD=90-\angle DBM\)
Tương tự \(\Rightarrow MEFC\) nội tiếp \(\Rightarrow\angle FEC=\angle FMC=90-\angle MCA\)
mà \(\angle DBM=\angle MCA\) (ABMC nội tiếp)
\(\Rightarrow\angle BED=\angle CEF\) mà B,E,C thẳng hàng \(\Rightarrow D,E,F\) thẳng hàng
c) Ta có: \(\angle NKM=\angle BKM=\angle BCM=\angle EFM=\angle NFM\)
\(\Rightarrow MFKN\) nội tiếp mà \(MF\parallel NK(\bot AC)\)
\(\Rightarrow MFKN\) là hình thang cân \(\Rightarrow\angle MNH=\angle FKH=\angle FHK\) (K và H đối xứng qua AC)
\(\Rightarrow HF\parallel NM\) mà \(FM\parallel NH\) \(\Rightarrow MNHF\) là hình bình hành
có MN và HF là 2 đường chéo cắt nhau tại I
\(\Rightarrow I\) là trung điểm MH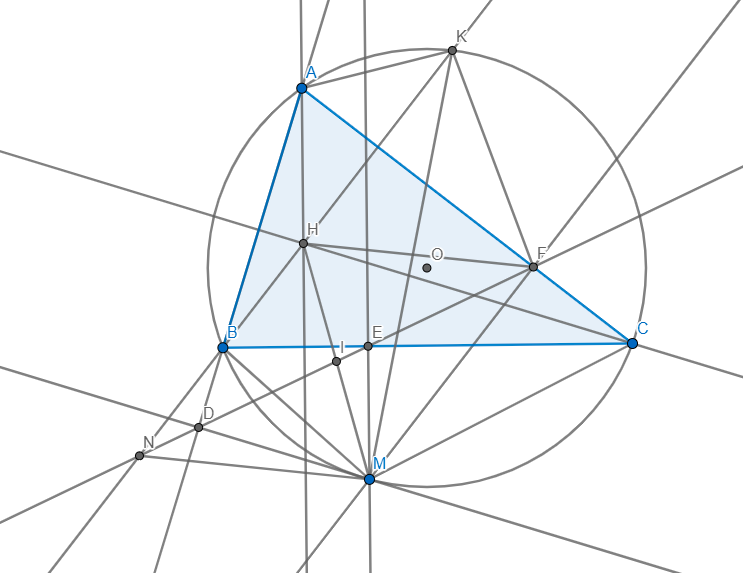

a) Có ^AOB = 1800 - ^OAB - ^OBA = 1800 - ^BAC/2 - ^ABC/2 = 900 + (1800 - ^BAC - ^ABC)/2 = 900 + ^ACB/2
b) Dễ thấy A,M,O,E cùng thuộc đường tròn đường kính OA (Vì ^AMO = ^AEO = 900) (1)
Ta có ^AOK = 1800 - ^AOB = 1800 - (900 + ^ABC/2) = 900 - ^ACB/2 = ^CEN (Do \(\Delta\)CEN cân tại C)
=> Tứ giác AOKE nội tiếp hay A,O,K,E cùng thuộc một đường tròn (2)
Từ (1) và (2) suy ra năm điểm A,M,K,O,E cùng thuộc một đường tròn (đpcm).
c) Ta thấy A,O,K,E cùng thuộc một đường tròn (cmt) và OK cắt AE tại T
Nên \(\frac{KT}{ET}=\frac{AT}{OT}\)(Hệ thức lượng đường tròn). Kết hợp \(\frac{AT}{OT}=\frac{AB}{OB}\)(AO là phân giác ^BAT)
Suy ra \(\frac{KT}{ET}=\frac{AB}{OB}\). Mặt khác: ^BKN = ^OAE = ^BAO và ^NBK = ^OBA => \(\Delta\)BKN ~ \(\Delta\)BAO (g.g)
=> \(\frac{AB}{OB}=\frac{KB}{NB}\). Từ đây \(\frac{KT}{ET}=\frac{KB}{BN}\)=> KT.BN = KB.ET (đpcm).
Hoàng Tử Hà, Nguyễn Thị Diễm Quỳnh, Nguyễn Thị Ngọc Thơ, Y, Hoàng Đình Bảo, DƯƠNG PHAN KHÁNH DƯƠNG, tran nguyen bao quan, huynh thi huynh nhu, HUYNH NHAT TUONG VY, Trương Thị Anh Quỳnh, Luân Đào, Phạm Hoàng Hải Anh, Nguyễn Việt Lâm, ...