Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em không vẽ được hình, xin thông cảm
a, Ta có góc EAN= cungEN=cung EC+ cung EN
Mà cung EC= cung EB(E là điểm chính giữa cung BC)
=> góc EAN=cungEB+ cung EN=góc DFE (tính chất góc ở giữa)
=> tam giác AEN đồng dạng tam giác FED
Vậy tam giác AEN đồng dạng tam giác FED
b,Ta có EC=EB=EM
Tam giác EMC cân tại E => EMC=ECM
MÀ EMC+AME=180, ECM+ABE=180
=> AME = ABE
=> tam giác ABE= tam giác AME
=> AB=AM => tam giác ABM cân tại A
Mà AE là phân giác => AE vuông góc BM
CMTT => AC vuông góc EN
MÀ AC giao BM tại M
=> M là trực tâm tam giác AEN
Vậy M là trực tâm tam giác AEN
c, Gọi H là giao điểm OE với đường tròn (O) (H khác E) => O là trung điểm của EH
Vì M là trực tâm của tam giác AEN
=> \(EN\perp AN\)
Mà \(OI\perp AN\)(vì I là trung điểm của AC)
=> \(EN//OI\)
MÀ O là trung điểm của EH
=> I là trung điểm của MH (đường trung bình trong tam giác )
=> tứ giác AMNH là hình bình hành
=> AH=MN
Mà MN=NC
=> AH=NC
=> cung AH= cung NC
=> cung AH + cung KC= cung KN
Mà cung AH+ cung KC = góc KMC(tính chất góc ở giữa 2 cung )
NBK là góc nội tiếp chắn cung KN
=> gócKMC=gócKBN
Hay gócKMC=gócKBM
=> CM là tiếp tuyến của đường tròn ngoại tiếp tam giác MBK( ĐPCM)
Vậy CM là tiếp tuyến của đường tròn ngoại tiếp tam giác BMK

a, Xét tứ giác CDME có
^MEC = ^MDC = 900
mà 2 góc này kề, cùng nhìn cạnh MC
Vậy tứ giác CDME là tứ giác nt 1 đường tròn
b, bạn ktra lại đề

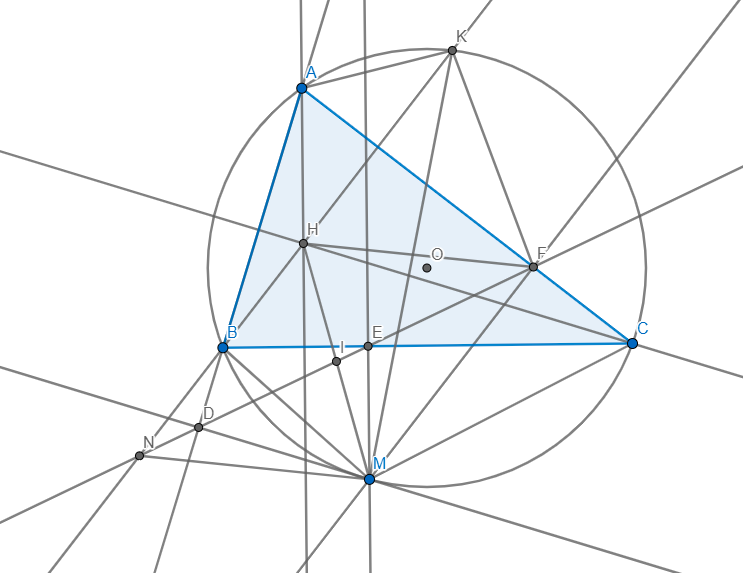
a) Ta có: \(\angle KAC=\angle KBC=90-\angle ACB=\angle HAC\)
mà \(AC\bot HK\Rightarrow\) H và K đối xứng với nhau qua AC
b) Ta có: \(\angle BEM+\angle BDM=90+90=180\Rightarrow BEMD\) nội tiếp
\(\Rightarrow\angle BED=\angle BMD=90-\angle DBM\)
Tương tự \(\Rightarrow MEFC\) nội tiếp \(\Rightarrow\angle FEC=\angle FMC=90-\angle MCA\)
mà \(\angle DBM=\angle MCA\) (ABMC nội tiếp)
\(\Rightarrow\angle BED=\angle CEF\) mà B,E,C thẳng hàng \(\Rightarrow D,E,F\) thẳng hàng
c) Ta có: \(\angle NKM=\angle BKM=\angle BCM=\angle EFM=\angle NFM\)
\(\Rightarrow MFKN\) nội tiếp mà \(MF\parallel NK(\bot AC)\)
\(\Rightarrow MFKN\) là hình thang cân \(\Rightarrow\angle MNH=\angle FKH=\angle FHK\) (K và H đối xứng qua AC)
\(\Rightarrow HF\parallel NM\) mà \(FM\parallel NH\) \(\Rightarrow MNHF\) là hình bình hành
có MN và HF là 2 đường chéo cắt nhau tại I
\(\Rightarrow I\) là trung điểm MH