Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

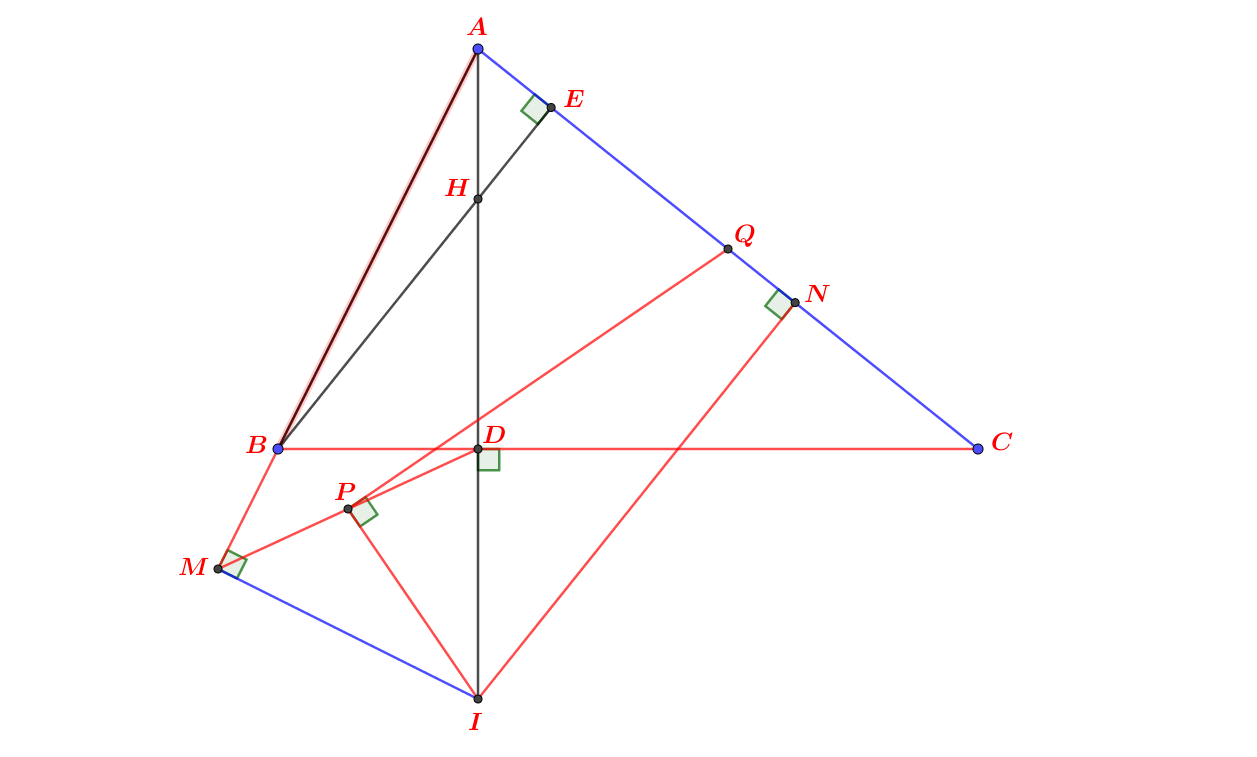
a) vì AD vuông góc BC => ADC = ADB =90
BE vuông góc AC => AEB = BEC =90
Xét tứ giác ABDE có
AEB = ADB =90 mà E và D là 2 đỉnh kề => tứ giác nt ( dhnb)
=> CAD = CBH (góc nt chắn ED) (1)
mà H đối xứng với I qua D => D là trung điểm => BD là trung tuyến của HI
ta lại có AD vuông góc BC tại D => BD vuông góc với HI ( H,I thuộc AD) => BD là đường cao của HI
xét tam giác BHI có
BD là trung tuyến của HI
BD là đường cao của HI
=> tam giác cân => BD là pg góc B = > IBC =CBH (2)
từ 1 và 2 => CAD = CBI
b) Xét tam giác AMI và tam giác ADB có
góc A chung
ADB = AMI =90
=> tam giác đồng dạng (gg) => ABD = AIM (2 góc tư) (3)
Gọi GD của CH và AB là F vì 2 đường cao AD và BE cắt nhau tại H => CH là đường cao => CF là đường cao => CF vuông góc AB tại F => CFB =90
xét tam giác CHD và tam giác CBF có
góc C chung
góc ADC = góc CFB =90
=> đồng dạng (gg)
=> CHD=CBA (2 góc tư) (4)
ta lại có vì CD vuông góc với HI
CD là trung tuyến của HI => tam giác CHI cân tại C => AIC = CHD (tc) (5)
từ 3-4-5 => AIM = AIC

a) Ta có tứ giác AIMJ là hcn=> AIMJ nội tiếp đường tròn đường kính AM, IJ
Vì N đối xứng với M qua IJ => góc JNI = góc JMI = 90o ha N thuộc đường tròn đường kính AM và IJ => góc ANM = 90o
mà I thuộc trung trực MN => tam giác MIC vuông cân tại I => I thuộc trung trực MC
=> I là tâm đường tròn ngoại tiếp tam giác MNC
=> góc MNC =1/2 góc MIC = 450
=> góc ABC + góc ANC = 45+90+45=1800
Hay tứ giác ABCN nội tiếp đường tròn (T) (ĐPCM)
b)CM: 1/PM<1/PB+1/PC ?
Ta có: tam giác MPC đồng dạng tam giác MBA => PM/MB=PC/BA => PM/PC=MB/BA (1)
TAM GIÁC MBP đồng dạng tam giác MAC => PM/MC=PB/CA=> PM/PB=MC/AC (2)
Cộng vế theo về của (1) và (2) ta có:
PM/PC+PM/PB=MB/BC+MC/AC=MB/BA+MC/BA=AC/BA>1 => ĐPCM
c) Áp dụng hệ thức giữa cạnh và đường cao ta có:
DH2=DK.DC => DA2=DK.DC
=> DA/DC=DK/DA => TAM GIÁC DKA đồng dạng tam giác DAC => góc AKD =DAC =45o
=> góc ABH+ góc AKH = 45+45+90=1800=> TỨ GIÁC ABHK nội tiếp
=> Góc AKB =AHB =90 = GÓC HKC
Mà góc ABK =AHK=KCH => đpcm

.Ta có :
AH⊥BC,HE⊥AB→\(\widehat{AEH}=\widehat{AHB}\)
=> \(\Delta AEH\approx\Delta AHB\)(g.g)
=>\(\dfrac{AE}{AH}=\dfrac{AH}{AB}\)
=>AH\(^2\)=AE.AB
Lam tuong tu ta dc AH\(^2\)=AF.AC
=> AE.AB=AF.AC
a: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nen AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB