Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y'=\dfrac{4.3}{8}.x^3+\dfrac{5.3}{6}x^2-\dfrac{2}{2\sqrt{x}}+3=\dfrac{3x^3}{2}+\dfrac{5x^2}{2}-\dfrac{1}{\sqrt{x}}+3\)

(Dòng khoanh đỏ ở dấu tương đương đầu tiên)Có nghĩa là chia cả hai vế cho \(\dfrac{5\pi}{3}\) ấy
(Dòng khoanh đỏ ở dấu tương đương thứ hai) Xét \(cos\pi x=\dfrac{1}{10}+k\dfrac{6}{5}\) (*)
Do \(-1\le cos\pi x\le1\)\(\Leftrightarrow-1\le\dfrac{1}{10}+k\dfrac{6}{5}\le1\)
\(\Leftrightarrow-\dfrac{11}{12}\le k\le\dfrac{3}{4}\) mà k nguyên \(\Rightarrow k=0\)
Thay k=0 vào (*)\(\Rightarrow cos\pi x=\dfrac{1}{10}\)
Làm tương tự với cái bên dưới \(-1\le\dfrac{1}{2}+k\dfrac{6}{5}\le1\) \(\Leftrightarrow-\dfrac{5}{4}\le k\le\dfrac{5}{12}\Rightarrow\left[{}\begin{matrix}k=0\\k=-1\end{matrix}\right.\)
Thay k=0 với k=-1 sẽ ra được \(\left[{}\begin{matrix}cos\pi x=\dfrac{1}{2}\\cos\pi x=-\dfrac{7}{10}\end{matrix}\right.\)
(Với mỗi \(cos\pi x\) sẽ nhận được hai họ nghiệm => Tổng tất cả là 6 họ nghiệm)
Vì \(cosx\in\left[-1;1\right]\Rightarrow\left[{}\begin{matrix}-1\le\dfrac{1}{10}+k\dfrac{6}{5}\le1\left(1\right)\\-1\le\dfrac{1}{2}+k\dfrac{6}{5}\le1\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow-\dfrac{11}{12}\le k\le\dfrac{9}{12}\Leftrightarrow k=0\Rightarrow cosx=\dfrac{1}{10}\)
\(\left(2\right)\Leftrightarrow-\dfrac{15}{12}\le k\le\dfrac{5}{12}\Leftrightarrow\left[{}\begin{matrix}k=0\\k=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\\cosx=-\dfrac{7}{10}\end{matrix}\right.\)

Vậy hãy sử dụng 1 phương pháp giải khác tối ưu hơn:
\(\Leftrightarrow2sin^22x=1\)
\(\Leftrightarrow1-2sin^22x=0\)
\(\Leftrightarrow cos4x=0\)
\(\Leftrightarrow4x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\)
Với cách giải này thì nghiệm được gộp luôn

Ta có : \(f\left(2\right)=2a+b-6\)
\(\lim\limits_{x\rightarrow2^+}\dfrac{x-\sqrt{x+2}}{x^2-4}=\lim\limits_{x\rightarrow2^+}\dfrac{x^2-x-2}{\left(x-2\right)\left(x+2\right)\left(x+\sqrt{x+2}\right)}\)
\(=\lim\limits_{x\rightarrow2^+}\dfrac{x+1}{\left(x+2\right)\left(x+\sqrt{x+2}\right)}=\dfrac{3}{16}\)
\(\lim\limits_{x\rightarrow2^-}x^2+ax+3b=4+2a+3b\)
H/s liên tục tại điểm x = 2 \(\Leftrightarrow\dfrac{3}{16}=2a+3b+4=2a+b-6\)
Suy ra : \(a=\dfrac{179}{32};b=-5\) => t = a + b = 19/32 . Chọn C

\(\left|cosx\right|=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\dfrac{\pi}{3}+k2\pi\\x=\pm\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{3}+k2\pi\)
\(\left|cosx\right|=\dfrac{1}{2}\)
\(\Leftrightarrow cos^2x=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{1+cos2x}{2}=\dfrac{1}{4}\)
\(\Leftrightarrow cos2x=-\dfrac{1}{2}\)
\(\Rightarrow2x=\pm\dfrac{2\pi}{3}+k2\pi\)
\(\Rightarrow x=\pm\dfrac{\pi}{3}+k\pi\)



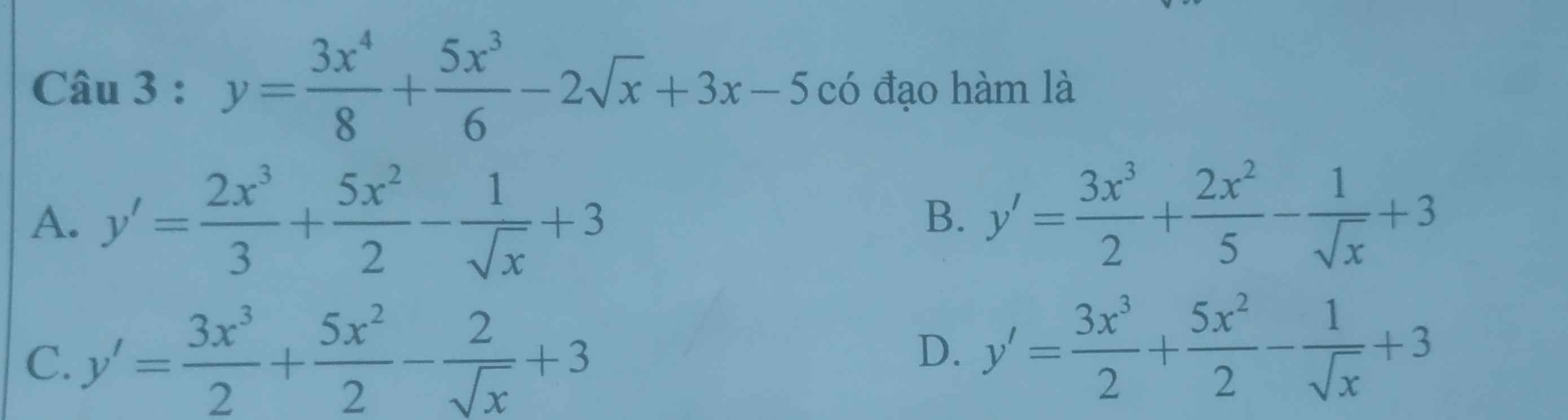 cho đáp án và giải thích giùm mình với ạ
cho đáp án và giải thích giùm mình với ạ