Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}\left(SAB\right)\cap\left(SAD\right)=SA\\\left(SAB\right)\perp\left(ABCD\right)\\\left(SAD\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
Gọi N là trung điểm BC \(\Rightarrow MN||AB\Rightarrow AB||\left(SMN\right)\)
\(\Rightarrow d\left(AB;SM\right)=d\left(AB;\left(SMN\right)\right)=d\left(A;\left(SMN\right)\right)\)
Từ A kẻ \(AH\perp SM\)
\(\left\{{}\begin{matrix}MN||AB\Rightarrow MN\perp AD\\SA\perp\left(ABCD\right)\Rightarrow SA\perp MN\end{matrix}\right.\) \(\Rightarrow MN\perp\left(SAD\right)\Rightarrow MN\perp AH\)
\(\Rightarrow AH\perp\left(SMN\right)\Rightarrow AH=d\left(A;\left(SMN\right)\right)\)
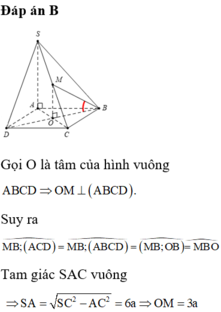
\(AC=a\sqrt{2}\Rightarrow SA=\sqrt{SC^2-AC^2}=a\)
\(AM=\dfrac{AD}{2}=\dfrac{a}{2}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AM^2}\Rightarrow AH=\dfrac{SA.AM}{\sqrt{SA^2+AM^2}}=\dfrac{a\sqrt{5}}{5}\)

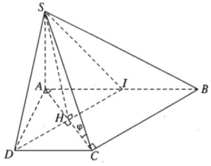
a) Ta có:
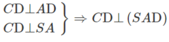
⇒ (SCD) ⊥ (SAD)
Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).
Vậy (SBC) ⊥ (SAC).
b) Ta có:
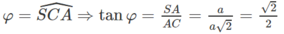
c) 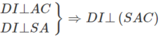
Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và 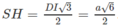 .
.
Tam giác SDI có diện tích:
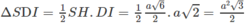

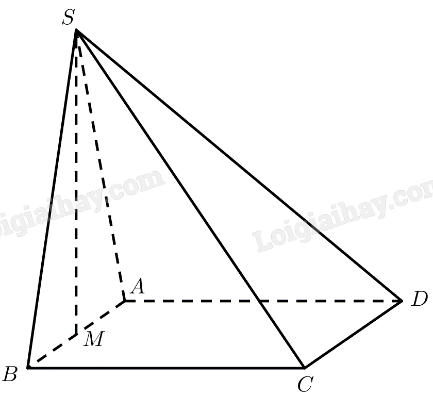
a, Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
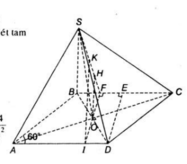

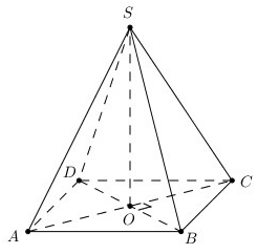


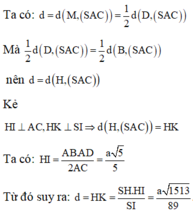

Gọi N là trung điểm AB \(\Rightarrow MN\perp AD\Rightarrow AD\perp\left(SMN\right)\Rightarrow AD\perp SM\)
Mặt khác: \(MN=AB=a\) ; \(SM=SN=\sqrt{SO^2+\left(\dfrac{MN}{2}\right)^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow SM^2+SN^2=MN^2\Rightarrow\Delta SMN\) vuông cân tại S hay \(SM\perp SN\)
\(\Rightarrow SM\perp\left(SAD\right)\)
Trong mp (SBC), dựng hình chữ nhật SMCP \(\Rightarrow CP||SM\Rightarrow CP\perp\left(SAD\right)\)
\(\Rightarrow\) SP là hình chiếu vuông góc của SC lên (SAD) hay \(\widehat{CSP}=\phi\)
\(AC=a\sqrt{5}\Rightarrow SC=\sqrt{SO^2+\left(\dfrac{AC}{2}\right)^2}=\dfrac{a\sqrt{6}}{2}\); \(SP=MC=\dfrac{BC}{2}=a\)
\(\Rightarrow CP=\sqrt{SC^2-SP^2}=\dfrac{a\sqrt{2}}{2}\)
\(sin\phi=\dfrac{CP}{SC}=\dfrac{\sqrt{3}}{3}\)