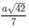

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Gọi N là trung điểm AB \(\Rightarrow MN\perp AD\Rightarrow AD\perp\left(SMN\right)\Rightarrow AD\perp SM\)
Mặt khác: \(MN=AB=a\) ; \(SM=SN=\sqrt{SO^2+\left(\dfrac{MN}{2}\right)^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow SM^2+SN^2=MN^2\Rightarrow\Delta SMN\) vuông cân tại S hay \(SM\perp SN\)
\(\Rightarrow SM\perp\left(SAD\right)\)
Trong mp (SBC), dựng hình chữ nhật SMCP \(\Rightarrow CP||SM\Rightarrow CP\perp\left(SAD\right)\)
\(\Rightarrow\) SP là hình chiếu vuông góc của SC lên (SAD) hay \(\widehat{CSP}=\phi\)
\(AC=a\sqrt{5}\Rightarrow SC=\sqrt{SO^2+\left(\dfrac{AC}{2}\right)^2}=\dfrac{a\sqrt{6}}{2}\); \(SP=MC=\dfrac{BC}{2}=a\)
\(\Rightarrow CP=\sqrt{SC^2-SP^2}=\dfrac{a\sqrt{2}}{2}\)
\(sin\phi=\dfrac{CP}{SC}=\dfrac{\sqrt{3}}{3}\)

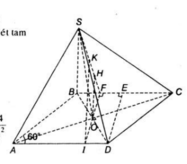
Do O là giao điểm 2 đường chéo \(\Rightarrow\) O là trung điểm AC và BD
Tam giác SAC cân tại S \(\Rightarrow SO\) là trung tuyến đồng thời là đường cao
\(\Rightarrow SO\perp AC\) (1)
Tương tự ta có \(SO\perp BD\) (2)
(1); (2) \(\Rightarrow SO\perp\left(ABCD\right)\)
b. Ta có \(AC\perp BD\) nên tam giác OBC vuông tại O
\(\Rightarrow OE=BE=\dfrac{1}{2}BC\) (trung tuyến ứng với cạnh huyền)
Mà \(\widehat{BCD}=\widehat{BAD}=60^0\Rightarrow\Delta BCD\) đều
\(\Rightarrow BD=BC\Rightarrow OB=BE=\dfrac{1}{2}BC\Rightarrow OB=OE=BE\)
\(\Rightarrow\Delta OBE\) đều \(\Rightarrow OF\perp BC\) (trung tuyến tam giác đều đồng thời là đường cao)
Mà \(SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
\(\Rightarrow BC\perp\left(SOF\right)\Rightarrow\left(SBC\right)\perp\left(SOF\right)\)

Đáp án D
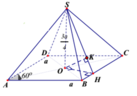
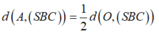
AC cắt (SBC) tại C , O là trung điểm AC =>khoảng cách
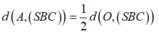
* Trong (ABCD) dựng OH ⊥ BC, trong (SOH) dựng OK ⊥ SH ta chứng minh được OK ⊥ (SBC)
=> khoảng cách d(O,(SBC))= OK.
∆ O B C vuông tại O có OH đường cao
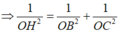
∆ S O H vuông tại O có OK đường cao
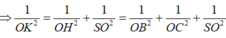
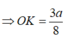
Vậy
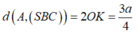

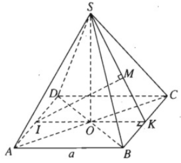
a) Gọi O là tâm hình vuông ABCD , dễ thấy I, O, K thẳng hàng. Vì K là trung điểm của BC nên SK ⊥ BC.
Ta có 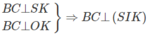
Do đó (SBC) ⊥ (SIK)
b) Hai đường thẳng AD và SB chéo nhau. Ta có mặt phẳng (SBC) chứa SB và song song với AD. Do đó khoảng cách giữa AD và SB bằng khoảng cách giữa AD và mặt phẳng (SBC).
Theo câu a) ta có (SIK) ⊥ (SBC) theo giao tuyến SK và khoảng cách cần tìm là IM, trong đó M là chân đường vuông góc hạ từ I tới SK. Dựa vào hệ thức IM. SK = SO. IK
ta có 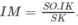
Ta lại có:
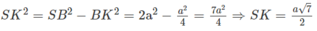
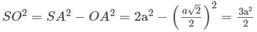
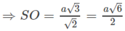
Do đó:
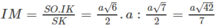
Vậy khoảng cách giữa hai đường thẳng AD và SB là bằng