Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
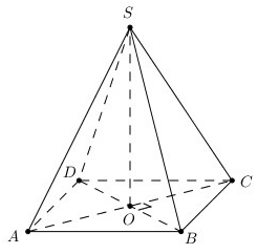
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được
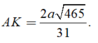

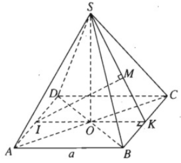
a) Gọi O là tâm hình vuông ABCD , dễ thấy I, O, K thẳng hàng. Vì K là trung điểm của BC nên SK ⊥ BC.
Ta có 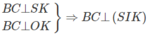
Do đó (SBC) ⊥ (SIK)
b) Hai đường thẳng AD và SB chéo nhau. Ta có mặt phẳng (SBC) chứa SB và song song với AD. Do đó khoảng cách giữa AD và SB bằng khoảng cách giữa AD và mặt phẳng (SBC).
Theo câu a) ta có (SIK) ⊥ (SBC) theo giao tuyến SK và khoảng cách cần tìm là IM, trong đó M là chân đường vuông góc hạ từ I tới SK. Dựa vào hệ thức IM. SK = SO. IK
ta có 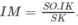
Ta lại có:
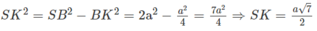
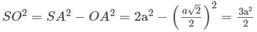
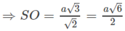
Do đó:
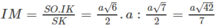
Vậy khoảng cách giữa hai đường thẳng AD và SB là bằng 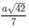


Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
E=AB∩CD,G=EN∩SB⇒GE=AB∩CD,G=EN∩SB⇒G là trọng tâm tam giác SAE.
d(M,(NCD))=GMGBd(B,(NCD))=12d(B,(NCD))=12.12d(A,(NCD))=14d(A,(NCD))=14hd(M,(NCD))=GMGBd(B,(NCD))=12d(B,(NCD))=12.12d(A,(NCD))=14d(A,(NCD))=14h
Tứ diện AEND vuông tại đỉnh A nên 1h2=1AN2+1AE2+1AD2=116a2⇒h=a√66111h2=1AN2+1AE2+1AD2=116a2⇒h=a6611
Vậy d(M,(NCD))=a√6644.d(M,(NCD))=a6644.

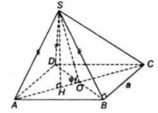
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
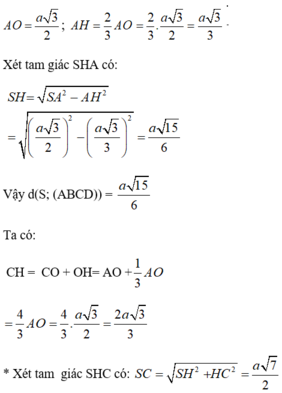


Gọi N là trung điểm AB \(\Rightarrow MN\perp AD\Rightarrow AD\perp\left(SMN\right)\Rightarrow AD\perp SM\)
Mặt khác: \(MN=AB=a\) ; \(SM=SN=\sqrt{SO^2+\left(\dfrac{MN}{2}\right)^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow SM^2+SN^2=MN^2\Rightarrow\Delta SMN\) vuông cân tại S hay \(SM\perp SN\)
\(\Rightarrow SM\perp\left(SAD\right)\)
Trong mp (SBC), dựng hình chữ nhật SMCP \(\Rightarrow CP||SM\Rightarrow CP\perp\left(SAD\right)\)
\(\Rightarrow\) SP là hình chiếu vuông góc của SC lên (SAD) hay \(\widehat{CSP}=\phi\)
\(AC=a\sqrt{5}\Rightarrow SC=\sqrt{SO^2+\left(\dfrac{AC}{2}\right)^2}=\dfrac{a\sqrt{6}}{2}\); \(SP=MC=\dfrac{BC}{2}=a\)
\(\Rightarrow CP=\sqrt{SC^2-SP^2}=\dfrac{a\sqrt{2}}{2}\)
\(sin\phi=\dfrac{CP}{SC}=\dfrac{\sqrt{3}}{3}\)

S A B C D H O K I L T
a) SA vuông góc với (ABCD) => SA vuông góc AD; hình thang ABCD vuông tại A => AD vuông góc AB
=> AD vuông góc (SAB), mà AD nằm trong (SAD) nên (SAB) vuông góc (SAD).
b) AD vuông góc (SAB), BC || AD => BC vuông góc (SAB) => B là hc vuông góc của C trên (SAB)
=> (SC,SAB) = ^CAB
\(SB=\sqrt{AS^2+AB^2}=\sqrt{2a^2+a^2}\)\(=a\sqrt{3}\)
\(\tan\widehat{CAB}=\frac{BC}{SB}=\frac{a}{a\sqrt{3}}=\frac{\sqrt{3}}{3}\)=> (SC,SAB) = ^CAB = 300.
c) T là trung điểm của AD, K thuộc ST sao cho AK vuông góc ST, BT cắt AC tại O, HK cắt AO tại I, AI cắt SC tại L.
BC vuông góc (SAB) => BC vuông góc AH, vì AH vuông góc SB nên AH vuông góc SC. Tương tự AK vuông góc SC
=> SC vuông góc (HAK) => SC vuông góc AI,AL. Lập luận tương tự thì AL,AI vuông góc (SCD).
Dễ thấy \(\Delta\)SAB = \(\Delta\)SAT, chúng có đường cao tương ứng AH và AK => \(\frac{HS}{HB}=\frac{KS}{KT}\)=> HK || BT || CD
=> d(H,SCD) = d(I,SCD) = IL (vì A,I,L vuông góc (SCD)) = \(\frac{IL}{AL}.AL=\frac{CO}{CA}.\frac{SI}{SO}.AL=\frac{1}{2}.\frac{SH}{SB}.\frac{AS.AC}{\sqrt{AS^2+AC^2}}\)
\(=\frac{1}{2}.\frac{SA^2}{SA^2+SB^2}.\frac{AS.AC}{\sqrt{AS^2+AC^2}}=\frac{1}{2}.\frac{2a^2}{2a^2+a^2}.\frac{a\sqrt{2}.a\sqrt{2}}{\sqrt{2a^2+2a^2}}=\frac{a}{3}\)