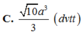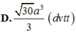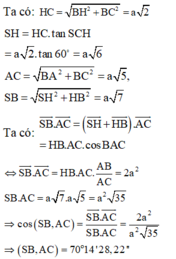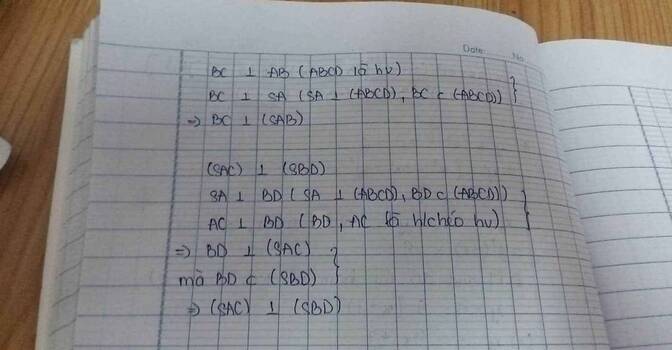Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

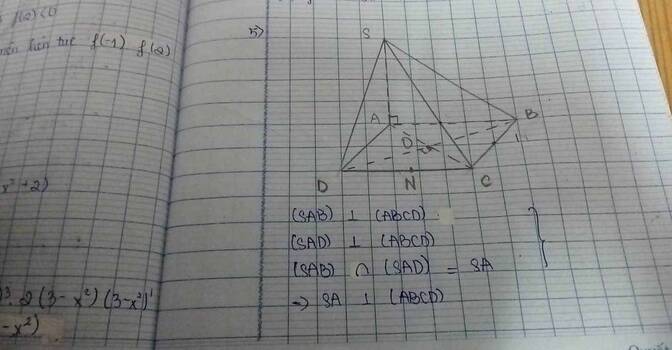
\(\left\{{}\begin{matrix}\left(SAB\right)\cap\left(SAD\right)=SA\\\left(SAB\right)\perp\left(ABCD\right)\\\left(SAD\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
Gọi N là trung điểm BC \(\Rightarrow MN||AB\Rightarrow AB||\left(SMN\right)\)
\(\Rightarrow d\left(AB;SM\right)=d\left(AB;\left(SMN\right)\right)=d\left(A;\left(SMN\right)\right)\)
Từ A kẻ \(AH\perp SM\)
\(\left\{{}\begin{matrix}MN||AB\Rightarrow MN\perp AD\\SA\perp\left(ABCD\right)\Rightarrow SA\perp MN\end{matrix}\right.\) \(\Rightarrow MN\perp\left(SAD\right)\Rightarrow MN\perp AH\)
\(\Rightarrow AH\perp\left(SMN\right)\Rightarrow AH=d\left(A;\left(SMN\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow SA=\sqrt{SC^2-AC^2}=a\)
\(AM=\dfrac{AD}{2}=\dfrac{a}{2}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AM^2}\Rightarrow AH=\dfrac{SA.AM}{\sqrt{SA^2+AM^2}}=\dfrac{a\sqrt{5}}{5}\)

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=45^0\Rightarrow AC=SA=a\sqrt{2}\)
\(\Rightarrow AB=a\)
Gọi N là trung điểm SA \(\Rightarrow NM||SB\Rightarrow SB||\left(DMN\right)\)
\(\Rightarrow d\left(DM;SB\right)=d\left(SB;\left(DMN\right)\right)=d\left(B;\left(DMN\right)\right)\)
Mà M là trung điểm AB \(\Rightarrow d\left(B;\left(DMN\right)\right)=d\left(A;\left(DMN\right)\right)\)
Từ A kẻ AH vuông góc DM \(\Rightarrow DM\perp\left(NAH\right)\)
Trong mp (NAH), từ A kẻ \(AK\perp NH\Rightarrow AK=d\left(A;\left(DMN\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AM^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{AM.AD}{\sqrt{AM^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AN^2}+\dfrac{1}{AH^2}\Rightarrow AK=\dfrac{AN.AH}{\sqrt{AN^2+AH^2}}=\dfrac{a\sqrt{7}}{7}\)

Đáp án C
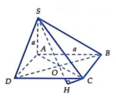
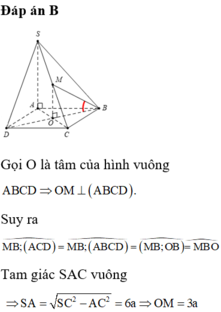
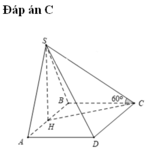
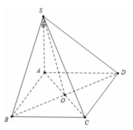
Gọi H là hình chiếu của C trên SO(O = AC ∩ BD), vì góc SOC tù nên H nằm ngoài SO
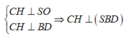
=> Góc tạo bởi SC và (SBD) là C S O ^
Ta có ![]()
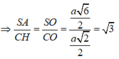
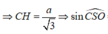
![]()

a) (SAB) và (SAD) cùng vuông góc (ABCD), (SAB) và (SAB) có giao tuyến SA => SA vuông góc (ABCD)
=> BC vuông góc SA. Mà BC vuông góc AB nên BC vuông góc (SAB).
Ta cũng có BD vuông góc AS, BD vuông góc AC vì ABCD là hình vuông
=> BD vuông góc (SAC) hay (SAC) vuông góc (SBD).
b) Gọi M là trung điểm của AB, CM cắt AD tại P, H thuộc CM sao cho AH vuông góc CM, K thuộc SH sao cho AK vuông góc SH.
Dễ thấy AN || CM => AN || (SCM) => d(AN,SC) = d(AN,SCM) = d(A,SCM) = d(A,SMP)
Ta có AH vuông góc MP, MP vuông góc AS => MP vuông góc (HAS) => (SMP) vuông góc (HAS)
Vì (SMP) và (HAS) có giao tuyến SH, AK vuông góc SH tại K nên d(A,SMP) = AK
Theo hệ thức lượng thì: \(\frac{1}{AK^2}=\frac{1}{AS^2}+\frac{1}{AM^2}+\frac{1}{AP^2}\)
\(\Rightarrow d\left(AN,SC\right)=d\left(A,SMP\right)=AK=\frac{AS.AM.AP}{\sqrt{AS^2AM^2+AM^2AP^2+AP^2AS^2}}\)
\(=\frac{a\sqrt{2}.\frac{a}{2}.a}{\sqrt{2a^2.\frac{a^2}{4}+\frac{a^2}{4}.a^2+a^2.2a^2}}=\frac{a\sqrt{22}}{11}.\)

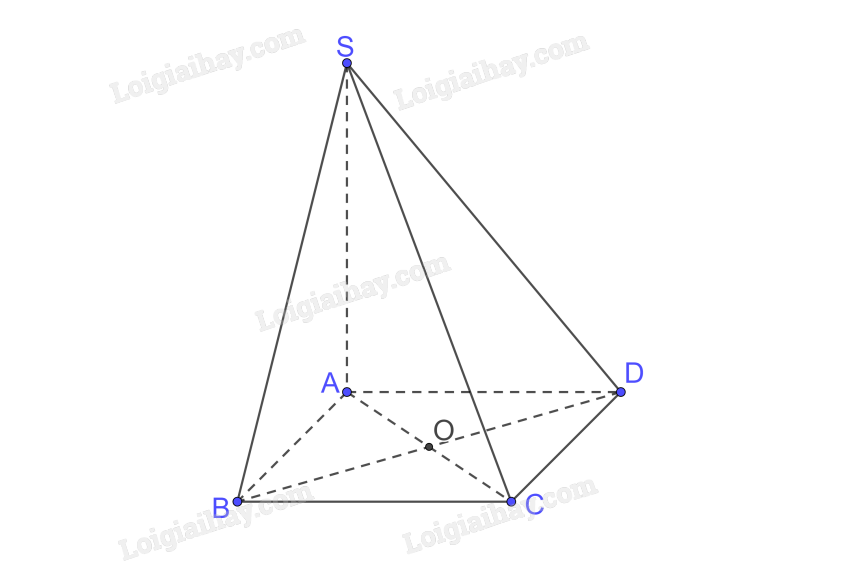
a) A là hình chiếu của S trên (ABCD) \(\left( {SA \bot \left( {ABCD} \right)} \right)\)
C là hình chiếu của C trên (ABCD)
\( \Rightarrow \) AC là hình chiếu của SC trên (ABCD)
\( \Rightarrow \) \(\left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)
Xét tam giác SAC vuông tại A có
\(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{a\sqrt 2 }}{{a\sqrt 2 }} = 1 \Rightarrow \widehat {SCA} = {45^0}\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {45^0}\)
b) \(\left. \begin{array}{l}AC \bot BD\left( {hv\,\,ABCD} \right)\\SA \bot BD\left( {SA \bot \left( {ABCD} \right)} \right)\\AC \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow \left( {BD,\left( {SAC} \right)} \right) = {90^0}\)
c) Gọi \(AC \cap BD = \left\{ O \right\}\) mà \(BD \bot \left( {SAC} \right)\)
\( \Rightarrow \) O là hình chiếu của B trên (SAC)
S là hình chiếu của S trên (SAC)
\( \Rightarrow \) SO là hình chiếu của SB trên (SAC).