K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
1 tháng 7 2018
ΔBDC có BE = ED và BM = MC
⇒ EM là đường trung bình của ΔBDC
⇒ EM // DC hay EM // DI.
ΔAEM có DI // EM (cmt) và AD = DE (gt)
⇒ IA = IM (Theo định lý 1)
5 tháng 8 2018
△BDC có ED = EB
MB = MC
⇒ EM là đường trung bình của tam giác này (Theo định nghĩa: đoạn thẳng nối trung điểm hai cạnh của một tam giác là đường trung bình của tam giác đó) ⇒ ME//CD
△AME có DA = DE (gt)
DI//ME (cmt)
⇒ IA = IM (Theo định lí: đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ 3)
NH
25 tháng 9 2017
\(\Delta BDC\) có BE=ED và BM=MC
nên EM// CD
\(\Rightarrow DI//EM\)
\(\Delta AEM\) có AD=DE và DI//EM
nên AI//IM
28 tháng 9 2017
t/g DBC có :
ED = EB ( gt )
MB = MC ( gt )
Nên EM là đường trung bình của tam giác DBC
\(\Rightarrow\)EM // DC
T/g AEM có :
DA = DE ( gt )
DI // EM ( cmt , vì EM // DC )
Theo định lý 1 ta có :
AI = IM ( đpcm )
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
21 tháng 12 2023
a/ Ta có
\(AB\perp AC\left(gt\right)\Rightarrow AM\perp AC;IN\perp AC\left(gt\right)\) => AM//IN
\(AC\perp AB\left(gt\right)\Rightarrow AN\perp AB;IM\perp AB\left(gt\right)\) => AN//IM
=> AMIN là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{A}=90^o\)
=> AMIN là HCN
b/
Ta co
AM//IN (cmt) =>AB//IK
BK//AI (gt)
=> ABKI là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh) => BK=AI (cạnh đối hbh)
c/
Xét tg vuông ABC có
\(AI^2=BI.CI\) (Trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow3AI^2=3.BI.CI\) (1)
Xét tg vuông MBI có
\(BM^2=BI^2-MI^2\) (2) (Pitago)
Xét tg vuông NCI có
\(CN^2=CI^2-NI^2\) (3) (Pitago)
Cộng 2 vế của (1) (2) (3) ta có
\(3AI^2+BM^2+CN^2=BI^2+CI^2+3.BI.CI-\left(MI^2+NI^2\right)=\)
\(=\left(BI+CI\right)^2+BI.CI-\left(MI^2+NI^2\right)=\)
\(=BC^2+BI.CI-\left(MI^2+NI^2\right)\) (4)
Ta có
\(BI.CI=AI^2\left(cmt\right)\) (5)
Xét tg vuông AIN có
\(AI^2=AN^2+NI^2\)
Do AMIN là HCN (cnt) => AN=MI
\(\Rightarrow AI^2=MI^2+NI^2\) (6)
Thay (5) và (6) vào (4) ta có
\(3AI^2+BM^2+CN^2=BC^2+AI^2-AI^2\)
\(\Rightarrow BC^2=3AI^2+BM^2+CN^2\left(dpcm\right)\)
12 tháng 8 2023
a: Xét ΔABC có
M,I lần lượt là trung điểm của CB,CA
=>MI là đường trung bình
=>MI//AB và MI=AB/2
mà MI=MK/2
nên MK=AB
MI//AB
AB vuông góc AC
=>MI vuông góc AC
Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
=>AMCK là hình bình hành
mà AC vuông góc MK
nên AMCK là hình thoi
b: Xét tứ giác AKMB có
MK//AB
MK=AB
=>AKMB là hình bình hành
22 tháng 11 2023
a: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}\)
Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
nên AMCK là hình bình hành
Hình bình hành AMCK có MA=MC
nên AMCK là hình thoi
b: AMCK là hình thoi
=>AK//MC và AK=MC
AK//MC
M\(\in\)BC
Do đó: AK//MB
AK=MC
MC=MB
Do đó: AK=MB
Xét tứ giác AKMB có
AK//MB
AK=MB
Do đó: AKMB là hình bình hành
c; Để hình thoi AMCK trở thành hình vuông thì \(\widehat{KCM}=90^0\)
AMCK là hình thoi
=>CA là phân giác của \(\widehat{KCM}\)
=>\(\widehat{ACM}=\dfrac{1}{2}\cdot\widehat{KCM}=45^0\)
=>\(\widehat{ACB}=45^0\)
KM
10 tháng 9 2019
∆BDC có BE = ED và BM = MC
nên EM // DC
Suy ra DI // EM
∆AEM có AD = DE và DI // EM
nên AI = IM.
29 tháng 11 2023
a: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(MA=MC=MB=\dfrac{BC}{2}\)
Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
=>AMCK là hình bình hành
Hình bình hành AMCK có MA=MC
nên AMCK là hình thoi
b: AMCK là hình thoi
=>AK//MC và AK=MC
AK=MC
MB=MC
Do đó: AK=MB
AK//MC
M\(\in\)BC
Do đó: AK//MB
Xét tứ giác ABMK có
AK//BM
AK=BM
Do đó: ABMK là hình bình hành
=>AM cắt BK tại trung điểm của mỗi đường
mà O là trung điểm của AM
nên O là trung điểm của BK
=>B,O,K thẳng hàng
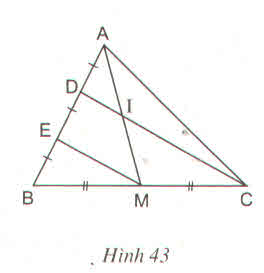
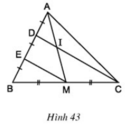
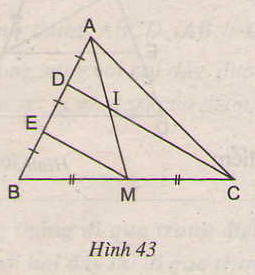
∆BDC có BE = ED và BM = MC
nên EM // DC
==> DI // EM
∆AEM có AD = DE và DI // EM
==> AI = IM.
Trong tam giác BAC có: EM là ĐTB nên DC // EM
ta có: I ∈ DC => DI // EM (DC // EM)
=> I là TĐ của AM nên AI = IM