K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
1 tháng 7 2018
ΔBDC có BE = ED và BM = MC
⇒ EM là đường trung bình của ΔBDC
⇒ EM // DC hay EM // DI.
ΔAEM có DI // EM (cmt) và AD = DE (gt)
⇒ IA = IM (Theo định lý 1)
5 tháng 8 2018
△BDC có ED = EB
MB = MC
⇒ EM là đường trung bình của tam giác này (Theo định nghĩa: đoạn thẳng nối trung điểm hai cạnh của một tam giác là đường trung bình của tam giác đó) ⇒ ME//CD
△AME có DA = DE (gt)
DI//ME (cmt)
⇒ IA = IM (Theo định lí: đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ 3)
NH
25 tháng 9 2017
\(\Delta BDC\) có BE=ED và BM=MC
nên EM// CD
\(\Rightarrow DI//EM\)
\(\Delta AEM\) có AD=DE và DI//EM
nên AI//IM
28 tháng 9 2017
t/g DBC có :
ED = EB ( gt )
MB = MC ( gt )
Nên EM là đường trung bình của tam giác DBC
\(\Rightarrow\)EM // DC
T/g AEM có :
DA = DE ( gt )
DI // EM ( cmt , vì EM // DC )
Theo định lý 1 ta có :
AI = IM ( đpcm )
DK
15 tháng 10 2021
Gọi E là trung điểm của DC
Trong ΔBDC, ta có:
M là trung điểm của BC (gt)
E là trung điểm của CD (gt)
Nên ME là đường trung bình của ∆ BCD
⇒ME // BD (tính chất đường trung bình tam giác)
Suy ra: DI // ME
AD = 1/2 DC (gt)
DE = 1/2 DC (cách vẽ)
⇒ AD = DE và DI//ME
Nên AI= IM (tính chất đường trung bình của tam giác).
G
21 tháng 7 2019
Hình bạn tự vẽ nhé
Giải: Kẻ \(MG//BD\) ta có: \(\hept{\begin{cases}MG//BD\\MB=MC\left(gt\right)\end{cases}}\Rightarrow\) MG là đường trung bình tam giác BCD.
\(\Rightarrow DG=CG=\frac{1}{2}CD\Rightarrow DG=AD\)
Xét tam giác AMG ta có: \(\hept{\begin{cases}MG//DI\\AD=DG\end{cases}}\Rightarrow AI=IM\left(đpcm\right)\) (tc đường tb tam giác)
DA
19 tháng 9 2017
Giải:
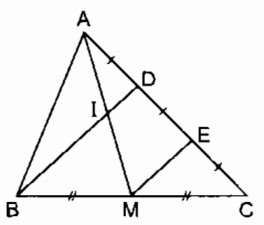
Gọi E là trung điểm của DC
Trong ∆ BDC ta có:
M là trung điểm của BC (gt)
E là trung điểm của CD (gt)
Nên ME là đường trung bình của ∆ BCD
⇒ ME // BD( tính chất đường trung bình của tam giác)
Suy ra: DI // ME
AD=\(\dfrac{1}{2}\)DC (gt)
DE=\(\dfrac{1}{2}\)DC (theo cách vẽ)
⇒AD = DE
DI // ME
Nên AI = IM (tính chất đường trung bình của tam giác)
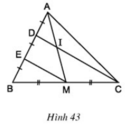
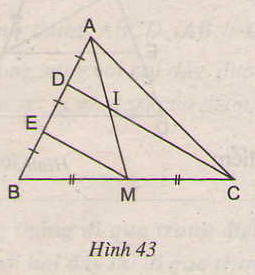
ai=im
∆BDC có BE = ED và BM = MC
nên EM // DC
Suy ra DI // EM
∆AEM có AD = DE và DI // EM
nên AI = IM.