Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Số kết quả xảy ra khi chọn ngẫu nhiên 3 sản phẩm là: \(C_{20}^3\) ( kết quả )
b) Chọn ngẫu nhiên 3 sản phẩm từ 20 sản phẩm ta được một tổ hợp chập 3 của 20. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{20}^3\)( phần tử)
Gọi A là biến cố “Cả 3 sản phẩm được chọn là chính phẩm”
Để chọn được cả 3 sản phẩm đều là chính phẩm thì ta phải chọn 3 sản phẩm từ 16 chính phẩm tức là ta được một tổ hợp chập 3 của 16 phần tử. Do đó số phần tử của biến cố A là: \(n\left( A \right) = C_{16}^3\)( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{16}^3}}{{C_{20}^3}} = \frac{{28}}{{57}}\).

Gọi p là tỉ lệ phế phẩm của kho hàng, với độ tin cậy \(\gamma\), khoảng tin cậy của p có dạng :
\(f_n-\frac{\sqrt{f_n\left(1-f_n\right)}}{\sqrt{n}}\Phi^{-1}\left(\frac{\gamma}{2}\right)< p< f_n+\frac{\sqrt{f_n\left(1-f_n\right)}}{\sqrt{n}}\Phi^{-1}\left(\frac{\gamma}{2}\right)\)(*)
Theo đề bài ta có: n= 400 \(\Rightarrow\sqrt{n}=20\)
\(f_n=\frac{20}{400}=0,05\); \(\gamma=0,95\Rightarrow\Phi^{-1}\left(\frac{\gamma}{2}\right)=\Phi^{-1}\left(0,475\right)=1,96\)
(*)\(\Leftrightarrow0,05-\frac{\sqrt{0,05.0,95}}{20}.1,96< p< 0,05+\frac{\sqrt{0,05.0,95}}{20}.1,96\)
\(\Leftrightarrow0,05-0,02< p< 0,05+0,02\)
\(\Leftrightarrow0,03< p< 0,07\)
Vậy khoảng tin cậy của tỉ lệ phế phẩm của kho hàng là : 0,03 < p < 0 ,07

Trong 11 ngày đầu làm được 11x112=1232(sp)
Trong 14 ngày sau làm được 14x125=1750(sp)
Cả tổ đã làm được 1232+1750=2982(sp)

Gọi số sản phẩm làm theo kế hoạch là \(x\) (sản phẩm)
=> Số ngày dự định làm xong là: \(\frac{x}{25}\) (ngày)
Số sản phẩm làm được sau khi cải tiến kĩ thuật là: \(x+10\) (sản phẩm)
=> Số ngày làm xong là: \(\frac{x+10}{30}\) (ngày)
Ta có: \(\frac{x}{25}-\frac{x+10}{30}=3\)
Giải phương trình đi bạn :)

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II sản xuất ra.
Như vậy tiền lãi có được là L = 3x + 5y (nghìn đồng).
Theo đề bài: Nhóm A cần 2x + 2y máy;
Nhóm B cần 0x + 2y máy;
Nhóm C cần 2x + 4y máy;
Vì số máy tối đa ở nhóm A là 10 máy, nhóm B là 4 máy, nhóm C là 12 máy nên x, y phải thỏa mãn hệ bất phương trình: 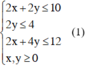
Khi đó bài toán trở thành: trong các nghiệm của hệ bất phương trình (1) thì nghiệm (x = xo; y = yo) nào cho L = 3x + 5y lớn nhất.
Miền nghiệm của hệ bất phương trình (1) là ngũ giác ABCDE kể cả miền trong.
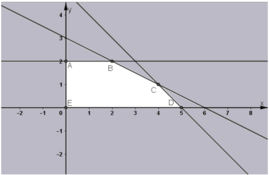
Ta có: L đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác ABCDE.
Tính giá trị của biểu thức L = 3x + 5y tại các đỉnh ta được:
Tại đỉnh A(0;2), L = 10
Tại đỉnh B(2; 2), L = 16
Tại đỉnh C(4; 1), L = 17
Tại đỉnh D(5; 0), L = 15
Tại đỉnh E(0; 0), L = 0.
Do đó, L = 3x + 5y lớn nhất là 17 (nghìn đồng) khi: x = 4; y = 1
Vậy để có tiền lãi cao nhất, cần sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm loại II.
Dễ thấy, X nhận các giá trị thuộc tập \(\left\{0;1;2\right\}\)
Xác suất để lấy ra 3 sản phẩm không có phế phẩm:
\(P\left(X=0\right)=\dfrac{C^0_2.C_4^{3-0}}{C^3_6}=\dfrac{1}{5}\)
Xác suất để lấy ra 2 sản phẩm không phế phẩm và 1 sản phẩm phế phẩm:
\(P\left(X=1\right)=\dfrac{C^1_2.C^{3-1}_4}{C^3_6}=\dfrac{3}{5}\)
Xác suất để lấy ra 1 sản phẩm không phế phẩm và 2 sản phẩm phế phẩm:
\(P\left(X=2\right)=\dfrac{C^2_2.C^{3-2}_4}{C^3_6}=\dfrac{1}{5}\)
bảng phân phối xác suất của X: