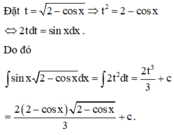nguyên hàm (xsinx+cosx)/(x^2-(cosx)^2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 9 2018
Ta có d y = x sin x + cos x ' d x = sin x + x cos x − sin x d x = x cos x d x
Chọn đáp án B.
CM
27 tháng 5 2019
y’= sinx + xcosx – sinx = xcosx
do đó dy= xcosxdx
Đáp án là A
PT
1
CM
26 tháng 6 2019
Ta có ∫ (xcosx)’dx = (xcosx) và ∫ cosxdx = sinx. Từ đó
∫ xsinxdx = - ∫ [(xcosx)’ – cosx]dx = -∫ (xcosx)’dx + ∫ cosxdx = - xcosx + sinx + C.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2023
\(y=\dfrac{xsinx}{tanx}+\dfrac{cosx}{tanx}=x.cosx+\dfrac{cos^2x}{sinx}=x.cosx+\dfrac{1}{sinx}-sinx\)
\(y'=cosx-x.sinx-\dfrac{cosx}{sin^2x}-cosx=-x.sinx-\dfrac{cosx}{sin^2x}\)
\(\Rightarrow y'+y.tan=-x.sinx-\dfrac{cosx}{sin^2x}+x.sinx+cosx\)
\(=cosx\left(1-\dfrac{1}{sin^2x}\right)=\dfrac{-cosx\left(1-sin^2x\right)}{sin^2x}=\dfrac{-cos^3x}{sin^2x}\)
SM
1
TQ
11 tháng 5 2017
thế 0 với pi vào pt ra 1 số âm 1 số dương => pht có 1 n.................................................................!
(0;pi)=(1;-8.89604401)