Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi K là giao điểm của AB và EF
O là giao điểm của AC và BD => OB = OD vì ABCD là hình chữ nhật
Ta có: EK // OB => \(\frac{EK}{OB}=\frac{AE}{AO}\)
EF//OD => \(\frac{EF}{OD}=\frac{AE}{AO}\)
=> \(\frac{EK}{OB}=\frac{EF}{OD}\) mà OD = OB
=> EK = EF mặt khác EH = EB ( H đối xứng với B qua E )
=> KBFH là hình bình hành
=> KB //=HF ( 1)
Ta lại có: KB //GD ( vì G thuộc DC ; AB //DC ; ABCD là hình chữ nhật )
và GK // BD ( giả thiết )
=> GKBD là hình bình hành
=> KB // = GD ( 2)
Từ ( 1) và (2) => HF // = GD
=> HFDG là hình bình hành có: ^FDG = 90 độ ( kề bù ^ADC = 90 độ )
=> HFDG là hình chữ nhật
=> HD = FG ( hai đường chéo bằng nhau)
Answer:
a) Gọi I và J là giao điểm các đường chéo của hình chữ nhật MDNF và hình chữ nhật ABCD
Tam giác IND và tam giác JCD là các tam giác cân \(\Rightarrow\widehat{N_1}=\widehat{D_1}\) và \(\widehat{C_1}=\widehat{D_2}\)
Mặt khác \(\widehat{N_1}=\widehat{D_2}\) (Hai góc đồng vị)
Vậy \(\widehat{C_1}=\widehat{D_1}\Rightarrow DF//AC\)
b) Tứ giác EIDJ là hình bình hành vì có các cạnh đối song song
Có: EJ = ID nhưng IF = ID \(\Rightarrow IF=EJ\)
Từ đó tứ giác EFIJ là hình bình hành \(\Rightarrow FE=IJ\left(1\right)\)
Mặt khác trong tam giác FBD: có FB // IJ (2)
Từ (1) và (2) => điểm E, điểm B, điểm F thẳng hàng
Mà EF = IJ và EB = IJ
=> E là trung điểm BF
a] Để chứng minh AF // BD, ta cần chứng minh tỉ số đồng dạng giữa các cặp cạnh tương ứng của hai tam giác ACF và BDE. Ta có:
AC/BD = AD/BE (vì AF // BD) AC/AD = BE/BD (vì AM // BD và BN // BD)
Từ hai tỉ số trên, ta có:
AC/AD = BE/BD
Vậy, ta đã chứng minh được AF // BD.
b] Để chứng minh E là trung điểm CF, ta cần chứng minh CE = EF và CF // AB. Ta có:
CE = AM (vì CE // AM và AC // BD) EF = BN (vì EF // BN và AC // BD)
Vậy, ta đã chứng minh được E là trung điểm CF.
Bạn tự vẽ hình nhé
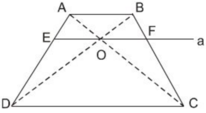
Xét \(\Delta ACD\) có OE // CD(gt)
=> \(\dfrac{OE}{DC}=\dfrac{AO}{AC}\left(1\right)\)
Xét \(\Delta BCD\) có OF // CD (gt)
=> \(\dfrac{OF}{DC}=\dfrac{BF}{FC}\left(2\right)\)
Mặt khác AB // CD nên \(\dfrac{AO}{AC}=\dfrac{BF}{FC}\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
=> \(\dfrac{OE}{DC}=\dfrac{OF}{DC}\) => OE = OF
Tam giác ABD có OE//AB
=>DO/DB = OE/AB (Theo hệ quả Đlý Ta-lét) (1)
Tam giác ABC có OF//AB
=>CO/CA = OF/AB (Theo hệ quả Đlý Ta-lét) (2)
Tam giác ABO có CD//AB
=>OD/OB = OC/OA (Theo hệ quả Đlý Ta-lét)
=> OD/(OB+OD) = OC/(OA+OC) hay OD/DB=CO/CA (3)
Từ (1) (2) và (3)
=> OE/AB = OF/AB
=> OE = OF (đpcm.)
Bạn tự vẽ hình nhé: nhớ **** cho mình với nhé...........
Gọi I và O thứ tự là giao điểm các đường chéo hình chữ nhật KMDN và ABCD.
Ta có: IN=ID=IK=IM ; OD=OC=OA=OB.
Do đó: góc N1=D1 ( tam giác NID cân do IN=ID )
góc D1=C1 ( tam giác DOC cân do OD=OC)
Mà góc N1=D1 ( đồng vị do EN song2 BD. Nên AC song2 KD.
Tứ giác EODI có EO song2 DI và EI song2 OD nên là hình bình hành.
=> OE=DI mà ID=KI nên OE=KI.
Tứ giác KEOI có KI song2 OE và KI song2 OE nên là hình bình hành.
=> KE song2 OI (1)
Tam giác KDB có OI là đường trung bình nên KB song2 OI (2)
Từ (1) và (2):=> K,E,B thẳng hàng ( tiên đề Euclide )
Câu hỏi của VO VAN BE SAU - Toán lớp 8 - Học toán với OnlineMath