cho tam giác ABC . trên cạnh BC lấy điểm M sao cho MB = MC = MA . C/M TAM GIÁC ABC vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trước tiên, ta có BM = BC theo đề bài. Vì tam giác ABC vuông tại A, nên ta có góc BAC = 90 độ.
Tiếp theo, ta biết rằng phân giác tam giác ABC cắt AC tại K. Vì vậy, ta có góc BAK = góc CAK.
Tương tự, phân giác tam giác ABC cắt MC tại I, nên ta có góc BAM = góc CAM.
Vì CN = MA, nên ta có góc CAN = góc CMA.
Từ các quan sát trên, ta có thể thấy rằng góc BAK = góc BAM = góc CAN = góc CMA.
Vì vậy, ta có thể kết luận rằng K, M, N thẳng hàng.
BN+NC=BC
BA+AM=BM
mà BC=BM và NC=AM
nên BN=BA
Xét ΔBAK và ΔBNK có
BA=BN
góc ABK=góc NBK
BK chung
Do đó: ΔBAK=ΔBNK
=>góc BNK=90 độ và KA=KN
Xét ΔKAM vuông tại A và ΔKNC vuông tại N có
KA=KN
AM=NC
Do đó; ΔKAM=ΔKNC
=>góc AKM=góc NKC
=>góc AKM+góc AKN=180 độ
=>K,M,N thẳng hàng

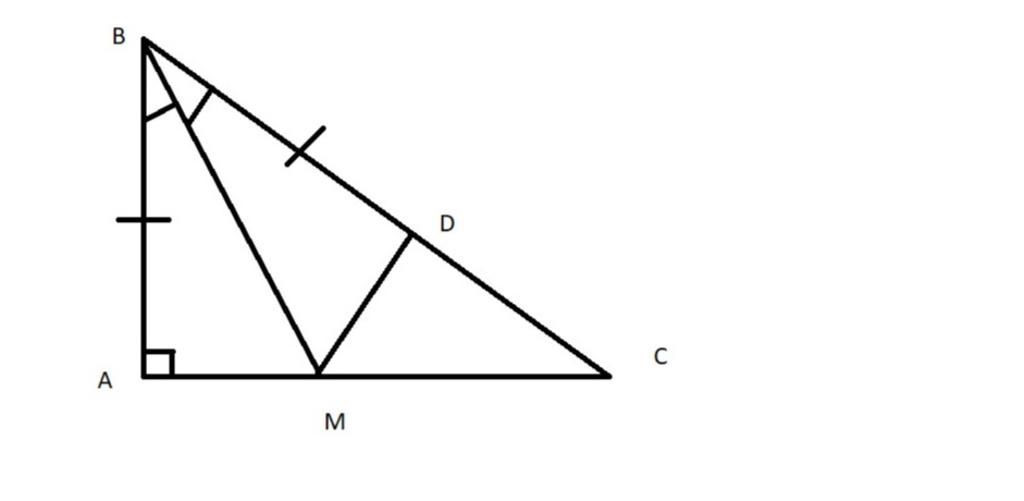

a)Xét △ABM và △△ DBM , ta có :
AB=BD(gt)
ˆABM^ == ˆDBM^ ( vì BM là tia phân giác của ˆABC^ )
BM là chung
⇒ △△ ABM= △△ DBM(c−g−c)
b)Ta có : ˆBAM^ == ˆBDM (( vì △ ABM= △ DBM)
Mà ˆBAM^ =90o(=90) ( vì △ ABC vuông tại A)
⇒⇒ ˆBDM=90o
⇒MD⇒ ⊥⊥ BC
c) Vì MD⊥⊥ BC(cmt)
⇒ ˆMDC^ =90o=90
⇒ △ MDC vuông tại D
⇒MC>MD(ch>cgv)
Mà MD=MA( vì △ABM=△ DBM)
⇒MC>MA

Xét tg ABM và tg ACM có chung đường cao hạ từ A xuống BC
\(\Rightarrow\frac{S_{ABM}}{S_{ACM}}=\frac{BM}{CM}=\frac{8}{4}=2\Rightarrow S_{ACM}=\frac{S_{ABM}}{2}=\frac{41,6}{2}=20,8cm^2\)
\(\Rightarrow S_{ABC}=S_{ABM}+S_{ACM}=41,6+20,8=62,4cm^2\)

Đáp án:
112,5cm²112,5cm²
Giải thích các bước giải:
[Ta có hình vẽ]
Vì AM=32MB⇒BM=2:(3+2)=25ABAM=32MB⇒BM=2:(3+2)=25AB
BN=2NC⇒BN=23BCBN=2NC⇒BN=23BC
+) Nối AA với NN
SBMN=25SABNSBMN=25SABN (vì đáy BM=25ABBM=25AB, chung chiều cao hạ từ N→ABN→AB)
SABN=23SABCSABN=23SABC (vì đáy BN=23ABBN=23AB, chung chiều cao hạ từ A→BCA→BC)
⇒SBMN=25×23=415SABC⇒SBMN=25×23=415SABC
SABCSABC =30:415=112,5(cm²)=30:415=112,5(cm²)
Đ/S: 112,5cm²