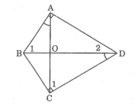
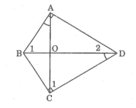
Tứ giác ABCD có hai góc vuông tại đỉnh A và C ,(BC < AD) AB cắt CD tại E . Hai đường chéo AC và BD cắt nhau tại O , góc BAO = góc BDC a, CM : Δ EAD đồng dạng với Δ ECB b, CM : OD . OB = OA . OC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 4 2017
Xét △ ABO và △ DCO,ta có:
∠ (BAO) = ∠ (BDC) (gt)
Hay ∠ (BAO) = ∠ (ODC)
∠ (AOB) = ∠ (DOC) (đối đỉnh)
Vậy △ ABO đồng dạng △ DCO (g.g)
CM
22 tháng 10 2019
Vì △ ABO đồng dạng △ DCO nên:
∠ B 1 = ∠ C 1 (1)
Mà ∠ C 1 = ∠ C 2 = ∠ (BCD) = 90 0 (2)
Trong △ ABD, ta có: ∠ A = 90 0
Suy ra: ∠ B 1 = ∠ D 2 = 90 0 (3)
Từ (1), (2) và (3): Suy ra: ∠ C 2 = ∠ D 2
Xét △ BCO và △ ADO, ta có:
∠ C 2 = ∠ D 2 (chứng minh trên)
∠ (BOC) = ∠ (AOD) (đối đỉnh)
Vậy △ BOC đồng dạng △ ADO (g.g).
8 tháng 7 2023
Xét ΔABO vuông tại O và ΔDCO vuông tại O có
góc BAO=góc CDO
=>ΔABO đồng dạng với ΔDCO
Xét ΔBCO vuông tại O và ΔADO vuông tại O có
góc OBC=góc OAD
=>ΔBCO đồng dạng với ΔADO
B1
14 tháng 8 2017
a, Chắc bạn vẫn còn nhớ phương pháp chứng mình 1 tứ giác là hình chữ nhật bằng cách chứng minh 2 đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường. Xét thấy tứ giác ABDC có tính chất như vậy nên nó là hình chữ nhật.
b,Xét tam giác AHB và tam giác BMA có góc AHb = góc BMA = 90 độ; cạnh AB chung; góc A = góc B (2 góc đáy của tam giác ABO cân tại O). => 2 tam giác này bằng nhau (cạnh huyền, góc nhọn) => BH = AM (cặp cạnh tương ứng). Xét tam giác ABO có AM/AO = BH/BO (do BH = AM và AO = BO).
=> MH song song với AB (định lý Ta - lét đảo). Mà AB vuông góc với AC nên suy ra HM vuông góc với AC.
c, Xét tam giác BHA và tam giác DNC có góc H = góc N = 90 độ; AB = CD và góc ABH = góc CDN => 2 tam giác này bằng nhau => BH = ND, tương tự cũng suy ra HN song song với BD (giống phần b). Do MH song song với AB; HN song song với BD => góc MHN = góc ABD = 90 độ (2 góc có cặp cạnh tương ứng song song thì bằng nhau nếu cùng nhọn, cùng tù hoặc có 1 góc vuông trong 2 góc ) => tam giác MHN vuông tại H => tâm đường tròn ngoại tiếp chình là trung điểm cạnh huyền và O chính là nó (hãy tự suy ra dựa vào những phần trên).
d, Gọi I là tâm đường tròn nội tiếp tam giác ABC vuông tại A, ta có tính chất sau r (bán kính đường tròn nội tiếp) = (AB + AC - BC)/2. Ta sẽ đi chứng minh điều này: Xét tam giác ABC vuông tại A có I là tâm đường tròn nội tiếp. Kẻ IH vuông góc với AB; IK vuông góc với AC và IL vuông góc với BC. => Ta chứng minh được r = AH = AK. BH = BL và CK = LC (hãy tự chứng minh bằng cách nôi A với I; B với I và C với I) => AH + AK = (AB - HB + AC - KC) = (AB + AC - BH - CK) = (AB + AC - BL - LC) = (AB + AC - BC) <=> 2r = (AB + AC - BC) => r = AB + AC - BC)/2 mà R = BC/2 (tính chất trong tam giác vuông) => R + r = AB + AC - BC)/2 + BC/2 = (AB + AC)/2. Mà AB + AC >hoặc= 2 nhân căn bậc 2 (AB.AC) => (AB + AC)/2 >hoặc= căn bậc 2 của(AB.AC) (đpcm)
24 tháng 6 2019
Câu hỏi của Nguyễn Thị Phương Uyên - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo link trên.
2 tháng 3 2023
a: Xét ΔBDE vuông tại D và ΔDCE vuông tại C có
góc E chung
=>ΔBDE đồng dạng với ΔDCE
b: Xét ΔHDC vuông tại H và ΔDBE vuông tại D có
góc HDC=góc DBE
=>ΔHDC đồng dạng với ΔDBE
=>DH/DB=CH/DE
=>DH*DE=CB*CH=DC^2
c: DC^2=CH*DB
=>CH*10=8^2=64
=>CH=6,4cm
\(DH=\sqrt{8^2-6.4^2}=4.8\left(cm\right)\)
=>DE=8^2/4,8=40/3(cm)
=>CE=32/3(cm)
Xét ΔHCE vuông tại H và ΔCDE vuông tại C có
góc HEC chung
=>ΔHCE đồng dạng với ΔCDE
=>\(\dfrac{S_{HCE}}{S_{CDE}}=\left(\dfrac{CE}{DE}\right)^2=\left(\dfrac{32}{3}:\dfrac{40}{3}\right)^2=\left(\dfrac{4}{5}\right)^2=\dfrac{16}{25}\)
