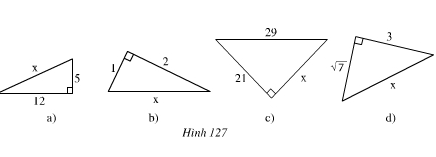
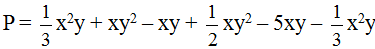Giaỉ giúp mình bài 53 sgk trang 27 toán 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


53. Tỉ số \(6\frac{1}{\frac{5}{5\frac{1}{6}}}\) có thể rút gọn như sau: \(6\frac{1}{\frac{5}{5\frac{1}{6}}}=\frac{6}{5}\)
-Thử lại : Ta có \(6\frac{1}{\frac{5}{5\frac{1}{6}}}\) = \(\frac{31}{\frac{5}{\frac{31}{6}}}\) = \(\frac{31}{5}.\frac{6}{31}=\frac{6}{5}\left(đúng\right)\)
-Ta có thể viết đươc lác tỉ số khác cũng có thể rút gọn như vậy.
Ví dụ: \(7\frac{1}{\frac{6}{6\frac{1}{7}}}=\frac{7}{6}\)hoặc\(9\frac{1}{\frac{5}{5\frac{1}{9}}}=\frac{9}{5}\)hoặc \(12\frac{1}{\frac{9}{9\frac{1}{12}}}=\frac{12}{9}\)



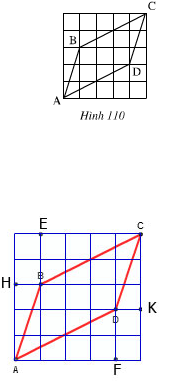
Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=>
hay DK là phân giác
=> =
∆ADI = ∆BDI (c.c.c)
=>
=> DI là phân giác
=> =
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay + = 900
Do đó + = 900
=> + = 1800
Xem thêm tại: http://loigiaihay.com/bai-55-trang-80-sgk-toan-lop-7-tap-2-c42a5841.html#ixzz44NZ9vg5o

Thu gọn rồi tính giá trị của đa thức P tại x = 0,5 và y = 1:

Giải:
∆AHB và ∆KBH có
AH=KH ( gt )
=
BH cạnh chung .
Nên ∆AHB=∆KBH(c.g.c)
Suy ra: =
Vậy BH là tia phân giác của góc B.
Tương tự ∆AHC =∆KHC ( c . g . c )
Suy ra: =
Vậy CH là tia phân giác của góc C
p/s: Very làm biếng open sách so copy mạng =]]]

+ ΔAHB và ΔCKD có
HB = KD (=1)
góc AHB = góc CKD(=90º)
AH = CK (=3).
⇒ ΔAHB = ΔCKD(c.g.c)
⇒AB = CD (hai cạnh tương ứng)
+ ΔCEB và ΔAFD có
BE = DF (=2)
góc BEC = góc DFA (=90º)
CE = AF (=4).
⇒ ΔCEB = ΔAFD ( c.g.c)
⇒ BC = AD (hai cạnh tương ứng)
b) ΔABD và ΔCDB có
AB = CD
AD = BC
BD cạnh chung
⇒ ΔABD = ΔCDB (c.c.c)
⇒ góc ABD = góc CDB (hai góc tương ứng)
Vậy AB // CD ( hai gó so le trong bằng nhau )
k minh nha
A B C D E F M N
(hình hơi xấu, thông cảm nha)
a) Xét \(\Delta AEB\)và \(\Delta DFC\) có:
AE = DF
\(\widehat{AEB}=\widehat{DFC}=90^o\)
BE = CF
Do đó: \(\Delta AEB=\Delta DFC\) (c.g.c)
Suy ra: AB = DC (đpcm)
Xét \(\Delta BMC\) và \(\Delta DNA\) có:
MC = NA
\(\widehat{BMC}=\widehat{DNA}=90^o\)
BM = DN
Do đó: \(\Delta BMC=\Delta DNA\)
Suy ra: BC = AD (đpcm)
b) Xét \(\Delta ABD\) và \(\Delta CDB\) có:
AB = CD (câu a)
BC = AD (câu a)
BD là cạnh chung
Do đó: \(\Delta ABD=\Delta CDB\) (c.c.c)
Suy ra: \(\widehat{ABD}=\widehat{CDB}\) (so le trong)
=> AB // CD (đpcm)