1,/x-5/+/y-3/=1
2,4x^3=4x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,=3x^2-6xy+3y^2-2x^2-4x-2-x^2+y^2\\ =4y^2-6xy-4x-2\\ b,=2\left(4x^2+20x+25\right)-3\left(1-16x^2\right)\\ =8x^2+40x+50-3+16x^2\\ =24x^2+40x+47\)


v) \(\left(-\dfrac{1}{2}x+3\right)\left(2x+6-4c^3\right)\)
\(=-\dfrac{1}{2}\left(2x+6-4c^3\right)+3\left(2x+6-4c^3\right)\)
\(=-x^2-3x+2c^3x+6x+18-12c^3\)
\(=-x^2+3x+2c^3x+18-12c^3\)
f) \(\left(2x-5\right)\left(x^2-x+3\right)\)
\(=2x\left(x^2-x+3\right)-5\left(x^2-x+3\right)\)
\(=2x^3-2x^2+6x-5x^2+5x-15\)
\(=2x^3-7x^2+11x-15\)
w) \(\left(3x+1\right)\left(x^2-2x-5\right)\)
\(=3x\left(x^2-2x-5\right)+\left(x^2-2x-5\right)\)
\(=3x^3-6x^2-15x+x^2-2x-5\)
\(=3x^3-5x^2-17x-5\)
x) \(\left(6x-3\right)\left(x^2+x-1\right)\)
\(=6x\left(x^2+x-1\right)-3\left(x^2+x-1\right)\)
\(=6x^3+6x^2-6x-3x^2-3x+3\)
\(=6x^3+3x^2-9x+3\)
y) \(\left(5x-2\right)\left(3x+1-x^2\right)\)
\(=5x\left(3x+1-x^2\right)-2\left(3x+1-x^2\right)\)
\(=15x^2+5x-5x^3-6x-2+2x^2\)
\(=-5x^3+17x^2-x-2\)
z) \(\left(\dfrac{3}{4}x+1\right)\left(4x^2+4x+4\right)\)
\(=\dfrac{3}{4}x\left(4x^2+4x+4\right)+\left(4x^2+4x+4\right)\)
\(=3x^3+3x^2+3x+4x^2+4x+4\)
\(=3x^3+7x^2+7x+4\)
f: =2x^3-2x^2+6x-5x^2+5x-15
=2x^3-7x^2+11x-15
w: =3x^3-6x^2-15x+x^2-2x-5
=3x^3-5x^2-17x-5
x: =6x^3+6x^2-6x-3x^2-3x+3
=6x^3+3x^2-9x+3
y: =(5x-2)(-x^2+3x+1)
=-5x^3+15x^2+5x+2x^2-6x-2
=-5x^3+17x^2-x-2
z: =3x^3+3x^2+3x+4x^2+4x+4
=3x^3+7x^2+7x+4

Tham khảo:
a)
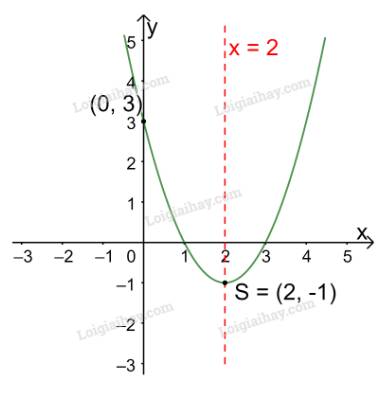
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = {x^2} - 4x + 3\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 = - 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
b)
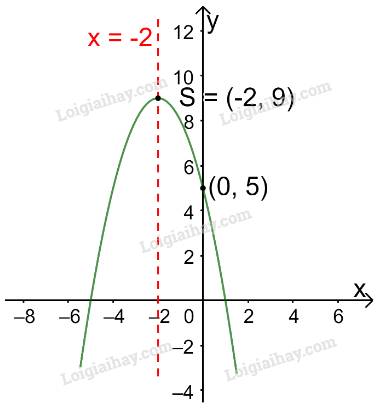
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} - 4x + 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.( - 1)}} = - 2;{y_S} = - {( - 2)^2} - 4.( - 2) + 5 = 9.\)
+ Có trục đối xứng là đường thẳng \(x = - 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).
Ta vẽ được đồ thị như hình dưới.
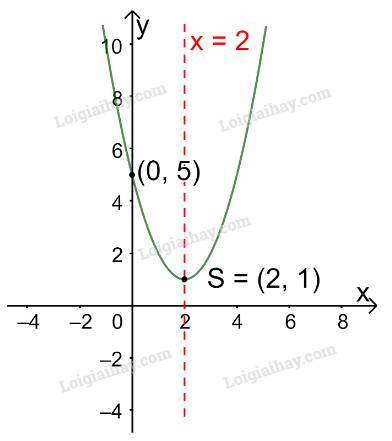
c) Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = {x^2} - 4x + 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 5 = 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).
Ta vẽ được đồ thị như hình dưới.
d)
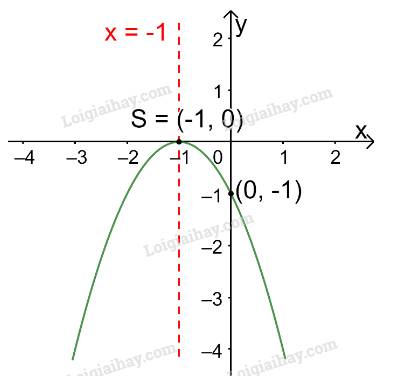
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} - 2x - 1\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 2)}}{{2.( - 1)}} = - 1;{y_S} = - {( - 1)^2} - 2.( - 1) - 1 = 0\)
+ Có trục đối xứng là đường thẳng \(x = - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua gốc tọa độ (0; -1).
Ta vẽ được đồ thị như hình dưới.

x^10 + x^5 + 1
= x^10 + x^9 - x^9 + x^8 - x^8 + x^7 - x^7 + x^6 - x^6 + x^5 + x^5 - x^5 + x^4 - x^4 + x^3 - x^3 + x^2 - x^2 + x - x + 1
= (x^10 + x^9 + x^8) - (x^9 + x^8 + x^7) + (x^7 + x^6 + x^5) - (x^6 + x^5 + x^4) + (x^5 + x^4 + x^3) - (x^3 + x^2 + x) + (x^2 + x + 1)
= x^8 (x^2 + x + 1) - x^7 (x^2 + x + 1) + x^5 (x^2 + x + 1) - x^4 (x^2 + x + 1) + x^3 (x^2 + x + 1) - x (x^2 + x + 1) + (x^2 + x + 1)
= (x^2 + x + 1) (x^8 - x^7 + x^5 - x^4 + x^3 - x + 1)
2. => 4x^3-4x = 0
=> 4x.(4x^2-1) = 0
=> x.(4x^2-1) = 0
=> x.(2x-1).(2x+1) = 0
=> x=0 hoặc 2x-1=0 hoặc 2x+1=0
=> x=0 hoặc x=1/2 hoặc x=-1/2
Vậy x thuộc {-1/2 ; 0 ; 1/2}
Tk mk nha
Laii quân heheeee