Tính số đo các góc của tam giác ACD như hình bên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 7 2017
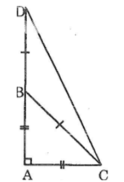
Ta có: ∆ABC vuông cân tại A
Suy ra: ∠ACB=∠ABC=45o
Lại có: ∆BCD vuông cân tại B (BC = BD)
Suy ra: ∠BCD=∠Dtính chất tam giác cân)
Trong ∆BCD ta có ∠ABC góc ngoài tại đỉnh B
Do vậy: ∠ABC=∠BCD + ∠D (tính chất góc ngoài của tam giác)
Suy ra: ∠ABC= ∠2∠BCD
Do đó: ∠BCD = 1/2 . ∠ABC = 1/2. 45º= 22º30’
=> ∠ACD = ∠ACB + ∠BCD = 45o+22o30'=67o30'
CM
19 tháng 1 2018
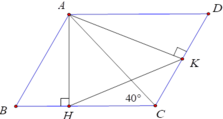
Vì AD.AH = AB.AK ( = S A B C D ) nên A H A K = A B A D = A B B C
Ta lại có AB // CD (vì ABCD là hình bình hành) mà AK ⊥ DC => AK ⊥ AB
=> BAK = 90 ∘ .
Từ đó góc HAK = ABC (cùng phụ với BAH)
Nên ΔAKH ~ ΔBCA (c.g.c) ⇒ A K H ^ = A C B ^ = 40 ∘
Đáp án: B
PT
0
D
27 tháng 1 2022
a) - Ta có: SABCD=AH.BC=AK.AB.
=>\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\)
- Ta có: \(\widehat{ABC}+\widehat{BAD}=180^0\) (AD//BC).
=>\(\widehat{ABC}+\widehat{BAH}+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(90^0+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(\widehat{HAK}+\widehat{KAD}=90^0\) mà \(\widehat{KAD}+\widehat{ADK}=90^0\) (tam giác ADK vuông tại K) nên \(\widehat{HAK}=\widehat{ADK}\) mà \(\widehat{ADK}=\widehat{ABC}\) (ABCD là hình bình hành) nên\(\widehat{HAK}=\widehat{ABC}\)
- Xét tam giác AKH và tam giác BCA có:
\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\) (cmt)
\(\widehat{HAK}=\widehat{ABC}\) (cmt)
=> Tam giác AKH ∼ Tam giác BCA (c-g-c).
b) - Ta có: Tam giác AKH ∼ Tam giác BCA (cmt) nên:
\(\widehat{AKH}=\widehat{ACB}=40^0\) (2 góc tương ứng)
27 tháng 5 2017
Ta có : AB=AC
=> \(\Delta ABC\) là tam giác vuông cân tại A ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{ABC}=A\widehat{CB}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{ABC}=A\widehat{CB}=45^0\)
=> \(\widehat{CBD}=\widehat{A}+\widehat{BCA}=135^0\) ( góc ngoài của tam giác )
Ta lại có:
BD=BC
=> \(\Delta BCD\) cân tại B ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{BDC}=\widehat{BCD}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{BDC}=\widehat{BCD}=\dfrac{\left(180^0-135^0\right)}{2}=\dfrac{45^0}{2}=22,5^0\)
Mà \(\widehat{ACD}=\widehat{BCA}+\widehat{BCD}\)
=> \(\widehat{ACD}=45^0+22,5^0=67,5^0\)
Vậy trong \(\Delta ACD\) có :
\(\left\{{}\begin{matrix}\widehat{A}=90^0\\\widehat{ADC}=22,5^0\\\widehat{ACD}=67,5^0\end{matrix}\right.\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Đặt \(a = BC,b = AC,c = AB\)
Ta có: \(a = 800,b = 700,c = 500.\)
Áp dụng định lí cosin, ta có:
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}.\)
Suy ra:
\(\begin{array}{l}\cos A = \frac{{{{700}^2} + {{500}^2} - {{800}^2}}}{{2.700.500}} = \frac{1}{7} \Rightarrow \widehat A = {81^o}47'12,44'';\\\cos B = \frac{{{{500}^2} + {{800}^2} - {{700}^2}}}{{2.500.800}} = \frac{1}{2} \Rightarrow \widehat B = {60^o};\\\cos C = \frac{{{{800}^2} + {{700}^2} - {{500}^2}}}{{2.800.700}} = \frac{{11}}{{14}} \Rightarrow \widehat C = {38^o}12'47,56''.\end{array}\)
Vậy \(\widehat A = {81^o}47'12,44'';\widehat B = {60^o};\widehat C = {38^o}12'47,56''.\)
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
Xét \(\Delta ABC\) ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} = 180^\circ \) (tính chất tổng ba góc trong tam giác)
Xét \(\Delta DAC\) ta có:
\(\widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ \)
Ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} + \widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ + 180^\circ \)
\(\widehat B + \widehat D + \left( {\widehat {BAC} + \widehat {DAC}} \right) + \left( {\widehat {BCA} + \widehat {DCA}} \right) = 360^\circ \)
\(\widehat B + \widehat D + \widehat {BAD} + \widehat {BCD} = 360^\circ \)
Vậy tổng các góc của tứ giác \(ABCD\) bằng \(360^\circ \)
Xét tam giác ABC,ta có:
AB=AC(theo hình vẽ)
góc BAC=90°(theo hình vẽ)
=>tam giác ABC vuông cân tại A
Nên: góc ABC=góc ACB
Mà: góc ABC+góc ACB=180°-góc BAC=180°-90°=90°
=>góc ABC=góc ACB=90°/2=45°
Mặt khác, ta lại có:
góc ABC+góc DBC=180°(2 góc kề bù)
=>góc DBC=180°-góc ABC=180°-45°=135°
Ta có: BD=BC(theo hình vẽ)
=>tam giác DBC cân tại B
=>góc BDC=góc BCD=45°/2=22,5°=góc ADC( vì A,B,D thẳng hàng)
=> góc ACD=góc ACB+góc BCD=45°+22,5°=67,5°.
Vậy các góc của tam giác ACD là:
góc CAD=90°
góc ACD=67,5°
góc ADC=22,5°