Cho x+y=2. CM rằng x2017+y2017\(\le\)x2018+y2018
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(2x^2+10y^2-6xy-6x-2y+10=0\)
\(\Leftrightarrow x^2-6xy+9y^2+x^2-6x+9+y^2-2y+1=0\)
\(\Leftrightarrow\left(x-3y\right)^2+\left(x-3\right)^2+\left(y-1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3y=0\\x-3=0\\y-1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
Vậy \(A=\dfrac{\left(x+y-4\right)^{2018}-y^{2018}}{x}=\dfrac{0^{2018}-1^{2018}}{3}=-\dfrac{1}{3}\)

Do \(x^2+y^2\ge0\) \(\forall x;y\Rightarrow x+y\ge0\)
Lại có \(x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\Rightarrow x+y\ge\frac{\left(x+y\right)^2}{2}\)
\(\Rightarrow2\left(x+y\right)-\left(x+y\right)^2\ge0\Rightarrow\left(x+y\right)\left(2-\left(x+y\right)\right)\ge0\)
- Nếu \(x+y=0\Rightarrow x+y< 2\) BĐT đúng
- Nếu \(x+y>0\Rightarrow2-\left(x+y\right)\ge0\Rightarrow x+y\le2\)
Vậy \(x+y\le2\)
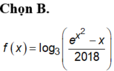
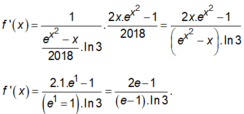
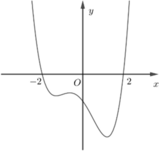
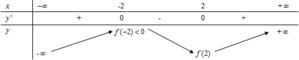

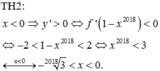
Ta có:
\(x^{2017}+y^{2017}\le x^{2018}+y^{2018}\) và x+y=2
Xét dấu =
Dấu ''='' xảy ra khi và chỉ khi
x=y=1
Dấu ''<'' xảy ra khi và chỉ khi x và y khác 1
Hết.
Em mới học lớp 7 nên ko biết đúng ko