Question

[Minh Vy Nguyên]

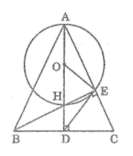
cho tam giác abc cân tại a có các đường cao AD BR cắt tại H . Vẽ đường tròn (O) đường kính AH=2R.

a) chứng minh E thuộc đường tròn (o)

b) DE là tiếp tuyến của đường tròn (O)

c) DE^2 = DH.DA

d) Gọi F là giao điểm của AB và đường tròn (O) . C , H ,F thẳng hàng

Answer 1

[Zed Of Gamer]

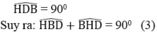
E dau tke

Answer 2

[Huy Hoang]

Tớ chỉ làm được mỗi câu a,b thôi nên bạn thông cảm =))

a) Vì OE = OA = OH nên':

=> E nằm trên đường tròn (O) có đường kính AH

b) Xét tam giác vuông BEC 

Có : ED là đường trung tuyến ứng với cạnh huyền

=> ED = DB

=> \(\widehat{E_1}=\widehat{B_1}\left(1\right)\)

Ta lại có : \(\widehat{E_2}=\widehat{H_1}=\widehat{H_2}\left(2\right)\)

Từ (1)(2) , suy ra :

\(\widehat{E_1}+\widehat{E_2}=\widehat{B_1}+\widehat{H_2}=90^o\)

Vậy : DE vuông góc với bán kính OE tại E nên DE là tiếp tuyến của đường tròn (O)