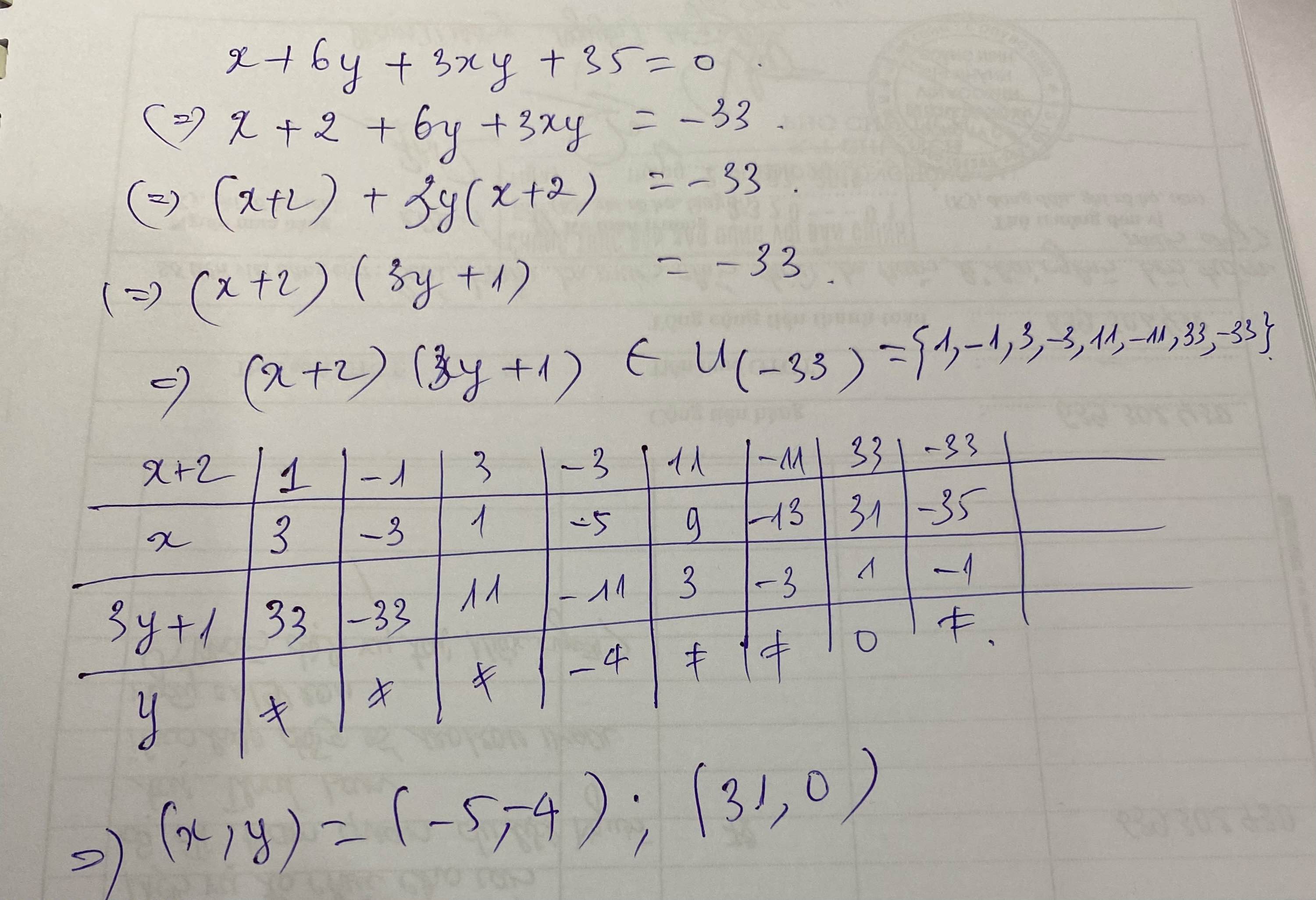3xy - 12 + 6y - 6x = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
K
0
HT
0
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 10 2020
a/ \(=x\left(x-4\right)-y\left(x-4\right)=\left(x-y\right)\left(x-4\right)\)
b/ \(=x\left(x+2\right)-3y\left(x+2\right)=\left(x-3y\right)\left(x+2\right)\)
c/ \(=2x\left(x-3\right)-3y\left(x-3\right)=\left(2x-3y\right)\left(x-3\right)\)
18 tháng 7 2021
Ta có:x+6y+3xy+35=0
<=> x(1+3y)+2(1+3y)+33=0
<=> (1+3y)(x+2)=-33
Do \(y\in Z\Rightarrow3y⋮3\Rightarrow1+3y\) chia 3 dư 1
Mà trong các Ư(-33) chỉ có -11 và 1 là chia 3 dư 1
TH1.\(\left\{{}\begin{matrix}1+3y=1\\x+2=-33\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-35\end{matrix}\right.\)
TH2.\(\left\{{}\begin{matrix}1+3y=-11\\x+2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-4\\x=1\end{matrix}\right.\)
Vậy,(x;y)=(-35;0),(1;-4)
NP
2
10 tháng 4 2018
a/ vì |5x-10| lớn hơn hoặc bằng 0 với mọi x
|6y+12| lớn hơn hoặc bằng 0 với mọi y
suy ra |5x-10|+|6y+12| lớn hơn hoặc bằng 0
mà |5x-10|+|6y+12|=0
dấu bằng xảy ra khi : 5x-10=0 suy ra 5x=10 suy ra x=2
6y+12=0 suy ra 6y=-12 suy ra y=-2
Câu b làm tương tự nhé bạn ( mũ 2 lên thì lớn hơn hoặc bằng 0)
10 tháng 4 2018
a/ Để |5x-10| + |6y+12| = 0 thi
|5x-10| = 0 và |6y+12| = 0
5x=10+0=10 6y = 0+12=12
x =10:5 y= 12:6
x=2 y=2
Vay x=2 va y=2
14 tháng 1 2023
Sửa đề: Tìm cặp \(x,y\in Z\) thỏa mãn \(x^2+3xy+2y^2+3x+6y-4=0\).
\(x^2+3xy+2y^2+3x+6y-4=0\)
\(\Leftrightarrow x^2+2xy+xy+2y^2+3x+6y=4\)
\(\Leftrightarrow\left(x^2+2xy\right)+\left(xy+2y^2\right)+\left(3x+6y\right)=4\)
\(\Leftrightarrow x\left(x+2y\right)+y\left(x+2y\right)+3\left(x+2y\right)=4\)
\(\Leftrightarrow\left(x+2y\right)\left(x+y+3\right)=4\)
Vì \(x,y\in Z\Rightarrow\left(x+2y\right)\left(x+y+3\right)\in Z\)
Trường hợp 1: \(\left\{{}\begin{matrix}x+2y=1\\x+y+3=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\) (thỏa mãn)
Trường hợp 2: \(\left\{{}\begin{matrix}x+2y=4\\x+y+3=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-8\\y=6\end{matrix}\right.\) (thỏa mãn)
Trường hợp 3: \(\left\{{}\begin{matrix}x+2y=2\\x+y+3=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=3\end{matrix}\right.\) (thỏa mãn)
Trường hợp 4: \(\left\{{}\begin{matrix}x+2y=-2\\x+y+3=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-8\\y=3\end{matrix}\right.\) (thỏa mãn)
Vậy: \(\left(x,y\right)=\left[\left(1;0\right),\left(-8;6\right),\left(-4;3\right),\left(-8;3\right)\right]\)