cho tam giác ABC, AD là đường phân giác  (D thuộc BC). Biết tỉ số BD/DC=3/5, BC=9. Tính BD,DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 4 2018
* CMR :
Gọi I là giao điểm của BD và AE
a) BD là trung trực AE
Xét t/g ABD và t/g EBD có :
B1 = B2 ( t/g ph.giác )
AD chung
BAD = BED ( = 90 )
=> t/g ABD = T/g EBD ( ch.gn)
- Xét t/g ABI và T/g EBI có :
AB = BE ( t/g ABD = t/g EBD )
B1 = B2 ( t/c ph.giác )
AI chung
=> ABI = EBI ( c.gc)
- Ta có :
I1 + I2 = 180 ( kb )
mà I1 = I2 ( T/g ABI = T/g EBI )
=> I1 = I2 = 180/2= 90
=> BD là trung trực của AE
b) DF = DC
Xét t/g ADF và T/g EDC có :
DAF = DEC ( =90 )
AD = DE ( t/g ABD = EBD )
D1 = D2 ( đđ )
=> T/g DAF = DEC ( g.c.g )
=> DF = DC
c/ AD = DC
Ta có :
B1 = B2 ( gt )
=> AD = CD ( q.hệ giữa góc và cạnh đối diện )
11 tháng 5 2018
bạn có câu hỏi hay đó nhưng mình ko biết cách làm...hi...hi
HX
1
26 tháng 2 2022
Vì AD là phân giác nên
\(\dfrac{AB}{AC}=\dfrac{BD}{DC}\Rightarrow\dfrac{DC}{AC}=\dfrac{BD}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\dfrac{DC}{AC}=\dfrac{BD}{AB}=\dfrac{6}{12}=\dfrac{1}{2}\Rightarrow DC=4cm;DB=2cm\)
16 tháng 6 2023
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: ΔHBA đồng dạng với ΔABC
=>BH/BA=BA/BC
=>BA^2=BH*BC
25 tháng 3 2023
a: \(BC=\sqrt{21^2+28^2}=35\left(cm\right)\)
BD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=35/7=5
=>DB=15cm; DC=20cm
b: AH=21*28/35=16,8cm
c: Xet ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
NT
4
CM
27 tháng 5 2019
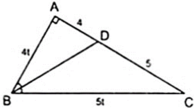
Áp dụng tính chất đường phân giác BD của tam giác
ABC, ta có:
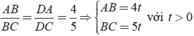với t > 0
Áp dụng định lý Py – ta – go ta có:
B C 2 = A C 2 + A B 2 hay ( 5 t ) 2 = 9 2 + ( 4 t ) 2 ⇔ ( 3 t ) 2 = 9 2 ⇒ t = 3 (vì t > 0 )
Khi đó: AB = 12cm, BC = 15cm