Mọi người hãy giúp tôi trả lời 2 bài này nha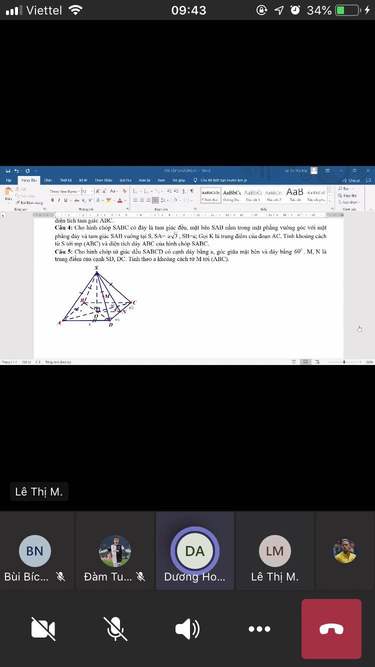
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




7,15 : 0,5 + 7,15 x 9 - 7,15
= 7,15 x 2 + 7,15 x 9 - 7,15
= 7,15 x ( 2 + 9 - 1 )
= 7,15 x 10
= 71,5
~ các bn thấy đúng thì hãy tk mk nha ~
Ta có:7,15 : 0,5 + 7,15 x 9 - 7,15
= 7,15 x 2 + 7,15 x 9 - 7,15
= 7,15 x ( 2+9-1)
= 7,15 x 10
= 71,5

nO2 = 5,6/22,4 = 0,25 (mol)
PTHH: 2KClO3 -> (t°, MnO2) 2KCl + 3O2
nKClO3 = 0,25 : 3 . 2 = 1/6 (mol)
nKClO3 = 1/6 . 122,5 = 245/12 (g)
nMg = 2,4/24 = 0,1 (mol)
PTHH: 2Mg + O2 -> (t°) 2MgO
LTL: 0,1/2 < 0,25 => O2 dư
nMgO = 0,1 (mol)
nMgO = 0,1 . 40 = 4 (g)
nO2 = 5,6 : 22,4 = 0,25(mol)
pthh : 2KClO3 -t--> 2KCl + 3O2
1/6 <----------------0,25(mol)
=>mKClO3 = 1/6.114,5=229/12(g)
nMg=2,4:24=0,1(mol)
pthh 2Mg+O2 -t-> 2MgO
0,1--------->0,1(mol)
=> mMgO = 0,1.40=4 (g)

1: Yes, I ( finish) .....finished.............. it an hour ago.
2: ...Have........they (pay )..paid..... money for your mother vet ?
3 ......Have.....you ever (eat )......eaten.......... Sushi?
4 Peter (play) ...played.......football yesterday.




Cái chữ nhìn muốn lé mắt :v
4/ Để tìm \(d\left(S,\left(ABC\right)\right)\) , ta phải hạ được đường vuông góc từ S xuống mp ABC. Nhận thấy \(\left(SAB\right)\perp\left(ABC\right)\) nên ta sẽ nghĩ ngay đến việc hạ đường vuông góc từ S xuống AB. Bởi dựa vô định lý sau: Khi 2 mp vuông góc thì mọi đường thẳng thuộc mp này và vuông góc với giao tuyến 2 mp thì nó sẽ vuông góc với mp còn lại.
Nên từ S ta kẻ \(SH\perp AB;SH\cap AB=\left\{H\right\}\Rightarrow SH\perp\left(ABC\right)\)
\(\Rightarrow SH=d\left(S,\left(ABC\right)\right)\)
\(SH=\dfrac{AS.SB}{\sqrt{AS^2+SB^2}}=....\)
5/ tìm khoảng cách từ M đến mp ABC, nghĩa là tÌm khoảng cách từ M đến mp ABCD
\(SM\cap\left(ABCD\right)=\left\{D\right\}\Rightarrow\dfrac{d\left(S,\left(ABCD\right)\right)}{d\left(M,\left(ABCD\right)\right)}=\dfrac{DS}{DM}=2\)
Vì chóp SABCD đều nên SO sẽ chính là đường cao của chóp
\(\Rightarrow d\left(S,\left(ABCD\right)\right)=SO\)
\(\left(\left(SCD\right),\left(ABCD\right)\right)=\widehat{SNO}=60^0\Rightarrow SO=ON.\tan60^0=\dfrac{a}{2}.\sqrt{3}=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow d\left(M,\left(ABCD\right)\right)=\dfrac{a\sqrt{3}}{2.2}=\dfrac{a\sqrt{3}}{4}\)