Hai xe cùng khởi hành một lúc từ hai địa điểm A và B (đi ngược chiều), biết vận tốc xe chạy từ B đến A bằng 0,8 lần vận tốc xe chạy từ A đến B. Hai xe gặp nhau tại một địa điểm C cách A một khoảng bằng 20 km. Tính quãng đường AB ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hai xe gặp nhau sau \(8h30'-7h=1h30'=1,5h\)
Quãng đường xe A đi đc: \(S_A=54\cdot1,5=81km\)
Quãng đường xe B đi: \(S_B=42\cdot1,5=63km\)
Khoảng cách giữa hai điểm A và B:
\(S_{AB}=81+63=144km\)
Đến lúc 8h (tức 2 xe đã đi đc 1h) thì:
Quãng đường xe đi từ A: \(S_A=54\cdot1=54km\)
Quãng đường xe đi từ B: \(S_B=42\cdot1=42km\)
Khi đó hai xe cách nhau \(54-42=12km\)

Chọn B
Chọn gốc tọa độ tại A : x 01 =0, x 02 = 120 km
Chọn gốc thời gian lúc 2 xe cùng xuất phát.
Chiều dương hướng từ A sang B : v A = 40 km/h, v B = -20 km/h
⇒ Phương trình chuyển động của 2 xe: 

a)
$S_1 = 30t(km)$
$S_2 = 50t(km)$
Hai xe gặp nhau :
$30t + 50t = 120 \Rightarrow t = 1,5(h) = 90(phút)$
Vậy hai xe gặp nhau lúc : 7 giờ 40 phút + 90 phút = 10 giờ 10 phút
Hai xe gặp nhau tại vị trí cách A một khoảng là $1,5.30 = 45(km)$
b)
t = 8 giờ - 7 giờ 40 phút = 20 phút = \(\dfrac{1}{3}\)(h)
\(S_1=\dfrac{30.1}{3}=10\left(km\right)\\ S_2=\dfrac{50.1}{3}=\dfrac{50}{3}\left(km\right)\)
Khoảng cách hai xe là \(120-10-\dfrac{50}{3}=\dfrac{280}{3}\left(km\right)\)
c)
Nếu hai xe đã gặp nhau và cách nhau 40 km :
$120 + 40 = 30t + 50t \Rightarrow t = 2(h)$
Thời điểm hai xe thỏa mãn là : 7 giờ 40 phút + 2 giờ = 9 giờ 40 phút
Nếu hai xe chưa gặp nhau :
$120 = 30t + 50t + 40 \Rightarrow t = 1(h)$
Thời điểm hai xe thỏa mãn là : 7 giờ 40 phút + 1 giờ = 8 giờ 40 phút

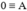 là
là