cho tam giấc ABC vuông tại A . tia phân giác của góc B cắt cạnh AC tại D . trên cạnh BC lấy điểm H sao cho BH = BA
a) chứng minh tam giác ABD = tam giác HBD
b) chứng minh DH vuông góc BC
c) giả sử góc C = \(60^o\) .tính số đo góc BDC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD và ΔBHD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔBAD=ΔBHD

a) Xét \(\Delta ABD\)và \(\Delta HBD\)có:
\(BA=BH\left(gt\right)\)
\(\widehat{ABD}=\widehat{HBD}\)(ad là tia phân giác của \(\widehat{B}\))
\(BD\)là cạnh chung
Do đó: \(\Delta ABD=\Delta HBD\left(c.g.c\right)\)

CM : a) Xét tam giác ABD và tam giác HBD
có AB = BD (gt)
góc DBA = góc HBD (gt)
BD : chung
=> tam giác ABD = tam giác HBD (c.g.c) (Đpcm)
b) Ta có : tam giác ABD = tam giác HBD (cm câu a)
=> góc A = góc DHB ( hai góc tương ứng)
Mà góc A =900 => góc DHB = 900
=> DH vuông góc với BC
c) Xét tam giác ABC có góc A = 900
=> góc B + góc C = 900 (t/c của 1 tam giác)
=> góc B = 900 - góc C = 900 - 360 = 540
Ta có : góc HBD = góc DBA = góc B/2 = 540/2 = 270
Xét tam giác ADE có A = 900
=> góc ADB + góc DBA = 900 (t/c của 1tam giác)
=> góc ADE = 900 - góc ADB = 900 - 270 = 630
(Em tự vẽ hình, ghi GT-KL nhé)
a) Xét \(\Delta ABD\)và \(\Delta HBD\)có:
AB = BH (gt)
^ABD = ^HBD (gt)
BD chung
=> \(\Delta ABD=\Delta HBD\left(c.g.c\right)\)
b) Ta có: \(\Delta ABD=\Delta HBD\left(cmt\right)\)
=> ^BAD = ^BHD = 90o
=> \(DH\perp BC\)
c)
\(\Delta ABC\)có : ^BAC + ^ABC + ^CBA = 180o
=> ^ABC = 180o- 90o- 36o = 54o
=> ^DBC = 1/2 ^ABC = 37o
\(\Delta BDC\): ^ADB là góc ngoài tại đỉnh D
=> ^ADB = ^DBC + ^DCB = 37o + 36o = 73o
Chúc em học tốt!!!

Xét ΔBAD và ΔBHD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔBAD=ΔBHD
=>\(\widehat{BAD}=\widehat{BHD}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BHD}=90^0\)
=>DH\(\perp\)HB
=>DH\(\perp\)BC

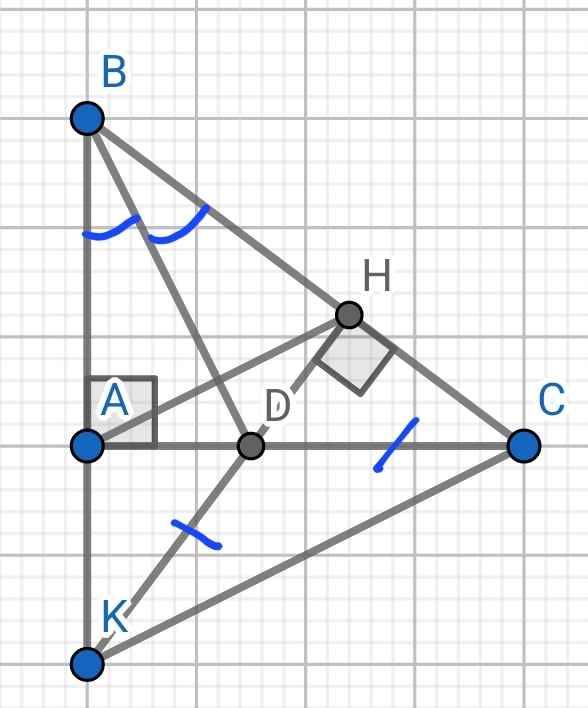
a) Xét hai tam giác vuông: ∆ABD và ∆HBD có:
BD chung
∠ABD = ∠HBD (BD là phân giác của ∠ABH)
⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)
b) Do ∆ABD = ∆HBD (cmt)
⇒ AB = BH (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AH (1)
Do ∆ABD = ∆HBD (cmt)
⇒ AD = HD (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AH
c) Xét ∆ADK và ∆HDC có:
AD = HD (cmt)
∠ADK = ∠HDC (đối đỉnh)
DK = DC (gt)
⇒ ∆ADK = ∆HDC (c-g-c)
⇒ ∠DAK = ∠DHC (hai góc tương ứng)
⇒ ∠DAK = 90⁰
Mà ∠DAB = 90⁰
⇒ ∠DAK + ∠DAB = 180⁰
⇒ B, A, K thẳng hàng

a: Xét ΔBAD và ΔBHD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔBAD=ΔBHD
Suy ra: \(\widehat{BAD}=\widehat{BHD}=90^0\)
hay DH\(\perp\)BC
b: \(\widehat{ABH}=180^0-110^0=70^0\)
nên \(\widehat{ABD}=\dfrac{70^0}{2}=35^0\)

a: Xét ΔABD vuông tạiA và ΔHBD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
b: BA=BH
DA=DH
=>BD là trung trực của AH
c: Xét ΔDAK và ΔDHC có
DA=DH
góc ADK=góc HDC
DK=DC
=>ΔDAK=ΔDHC
=>góc DAK=góc DHC=90 độ
=>góc DAK+góc DAB=180 độ
=>B,A,K thẳng hàng
Bn tự vẽ hình nha
a/ xét 🔼ABD và🔼HDB có:
AB=HB(GT)
ABD=DBH(do bd là phân giác của góc b)
cạnh BD chung
=>🔼ABD=🔼HDB(C.G.C)
b/ ta có 🔼ABD=🔼HDB( theo a)
<=>BAD= BDH=90 độ
=> dh vuông góc với bc
c/ vì tam giác ABC vuông tại A=> góc b + góc c = 90 độ => góc b = 30 độ
Vì db là phân giác của góc b=> gócDBC=15 độ
Xét tam giác DBC có DBC+DCB+BDC=180 độ ( định lí tổng 3 góc)
=> BDC=180-60-15=105 độ
Đúng hơm bn
giải quá nhanh,sai