chứng minh rằng : 2+22 + 23 ..... + 219 +220 +221 chia hết cho 14
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A=\((1+2)+\left(2^2+2^3\right)+...+\left(2^{19}+2^{20}\right)\)
A=\(3.1+2^2\left(1+2\right)+...+2^{19}\left(1+2\right)\)
A=\(3.1+3.2^2+...+3.2^{19}\)
A=\(3\left(1+2^2+...+2^{19}\right)\)\(⋮3\)
Vậy A\(⋮3\)
A=(1+2)+(22+23)+...+(219+220)(1+2)+(22+23)+...+(219+220)
A=3.1+22(1+2)+...+219(1+2)3.1+22(1+2)+...+219(1+2)
A=3.1+3.22+...+3.2193.1+3.22+...+3.219
A=3(1+22+...+219)3(1+22+...+219)⋮3⋮3
NÊN A⋮3

Sửa đề: \(A=2+2^2+2^3+2^4+...+2^{19}+2^{20}\)
=>\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{19}+2^{20}\right)\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{19}\left(1+2\right)\)
\(=3\left(2+2^3+...+2^{19}\right)⋮3\)

A = 2 + 22 + 23 + 24 + ... + 219 + 220
A = (2 + 22) + (23 + 24) +... + (219 + 220)
A = 2.(1+2) + 23.(1 + 2) +... + 219.(l + 2)
A = 2.3 + 23.3 +...+ 219.3 Do đó A chia hết cho 3


a) \(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{19}+2^{20}\right)\)
\(A=2\cdot\left(1+3\right)+2^3\cdot\left(1+3\right)+...+2^{59}\cdot\left(1+3\right)\)
\(A=3\cdot\left(2+2^3+...+2^{59}\right)\)
Vậy A chia hết cho 3
________
\(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^3\right)+\left(2^2+2^4\right)+...+\left(2^{58}+2^{60}\right)\)
\(A=2\cdot\left(1+4\right)+2^2\cdot\left(1+4\right)+...+2^{58}\cdot\left(1+4\right)\)
\(A=5\cdot\left(2+2^2+...+2^{58}\right)\)
Vậy A chia hết cho 5

a) A chia hết cho 2 vì tất cả các số hạng của tổng đều chia hết cho 2.
b) Ta tách ghép các số hạng của A thành các nhóm sao cho mỗi nhóm xuất hiện thừa số chia hết cho 3. Khi đó:

![]()
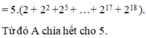

a: \(G=8^8+2^{20}\)
\(=2^{24}+2^{20}\)
\(=2^{20}\left(2^4+1\right)=2^{20}\cdot17⋮17\)
b: Sửa đề: \(H=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{59}\left(1+2\right)\)
\(=3\left(2+2^3+...+2^{59}\right)⋮3\)
\(H=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\left(2+2^4+...+2^{58}\right)⋮7\)
\(H=2+2^2+2^3+...+2^{60}\)
\(=\left(2+2^2+2^3+2^4\right)+...+\left(2^{57}+2^{58}+2^{59}+2^{60}\right)\)
\(=2\left(1+2+2^2+2^3\right)+...+2^{57}\left(1+2+2^2+2^3\right)\)
\(=15\left(2+2^5+...+2^{57}\right)⋮15\)
c: \(E=\left(1+3+3^2\right)+3^3\left(1+3+3^2\right)+...+3^{1989}\left(1+3+3^2\right)\)
\(=13\left(1+3^3+...+3^{1989}\right)⋮13\)
\(E=1+3+3^2+3^3+...+3^{1991}\)
\(=\left(1+3+3^2+3^3+3^4+3^5\right)+\left(3^6+3^7+3^8+3^9+3^{10}+3^{11}\right)+...+3^{1986}+3^{1987}+3^{1988}+3^{1989}+3^{1990}+3^{1991}\)
\(=364\left(1+3^6+...+3^{1986}\right)⋮14\)

Áp dụng hàng đơn vị , chia từng cặp , như vậy mỗi cặp có hàng đơn vị sẽ có dạng 1 + 2 + 3 + 4 + ..... + 10 = 55 và sẽ chia hết cho 5 .
Vậy M hoàn toàn chia hết cho 5 .
Tưởng ghi kiểu 2^1 + 2^2 + 2^3 + ... + 2^20 chứ ai dè ra đề bài dễ quá ta XD

Bài 1
a, cm : A = 165 + 215 ⋮ 3
A = 165 + 215
A = (24)5 + 215
A = 220 + 215
A = 215.(25 + 1)
A = 215. 33 ⋮ 3 (đpcm)
b,cm : B = 88 + 220 ⋮ 17
B = (23)8 + 220
B = 216 + 220
B = 216.(1 + 24)
B = 216. 17 ⋮ 17 (đpcm)
c, cm: C = 1 - 2 + 22 - 23 + 24 - 25 + 26 -...-22021 + 22022 : 6 dư 1
C=1+(-2+22-23+24- 25+26)+...+(-22017+22018-22019+22020-22021+22022)
C = 1 + 42 +...+ 22016.(-2 + 22 - 23 + 24 - 25 + 26)
C = 1 + 42+...+ 22016.42
C = 1 + 42.(20+...+22016)
42 ⋮ 6 ⇒ C = 1 + 42.(20+...+22016) : 6 dư 1 đpcm
Ta có: 2+22+23+24+...+219+220+221
= 2(1+2+22+23+...+220) chia hết cho 2 (1)
Lại có: 2+22+23+24+...+219+220+221
= 2(1+2+22)+...+219(1+2+22)
=2.7+24.7+...+219.7
=7(2+24+...+219) chia hết cho 7 (2)
Mà (2,7)=1 (3)
Từ 1,2,3 => 2+22+23+24+...+219+220+221 chia hết cho 14
Ta có: 2+22+23+24+...+219+220+221
= 2(1+2+22+23+...+220) chia hết cho 2 (1)
có: 2+22+23+24+...+219+220+221
= 2(1+2+22)+...+219(1+2+22)
=2.7+24.7+...+219.7
=7(2+24+...+219) chia hết cho 7 (2)
Mà (2,7)=1 (3)
Từ (1),(2),(3) => 2+22+23+24+...+219+220+221 chia hết cho 14(ddpcm)