0 : x = 0. Tìm x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 8 2021
1: Để A>0 thì x-1<0
hay x<1
Kết hợp ĐKXĐ, ta được: \(0\le x< 1\)
29 tháng 8 2021
1) Để A > 0 thì:
\(x-1< 0\Leftrightarrow x< 1\)
\(\Rightarrow0\le x< 1\) và \(x\ne1\)
2) \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=1+\dfrac{2}{\sqrt{x}-1}\)
Để A<1 thì \(\dfrac{2}{\sqrt{x}-1}< 0\)
\(\Rightarrow\sqrt{x}-1< 0\Leftrightarrow\sqrt{x}< 1\)
Mà x\(\ge0,x\ne1\)
\(\Rightarrow0\le x< 1\)
4 tháng 4 2022
d. Áp dụng BĐT Caushy Schwartz ta có:
\(x+y+\dfrac{1}{x}+\dfrac{1}{y}\le x+y+\dfrac{\left(1+1\right)^2}{x+y}=x+y+\dfrac{4}{x+y}\le1+\dfrac{4}{1}=5\)
-Dấu bằng xảy ra \(\Leftrightarrow x=y=\dfrac{1}{2}\)
TM
14 tháng 1
1. Khi \(m=-1\Rightarrow5x+2>0\Rightarrow x>-\dfrac{2}{5}\), suy ra \(f\left(x\right)>0\) không có tập nghiệm là \(R\).
Khi \(m\ne-1,f\left(x\right)>0\forall x\in R\) khi:
\(\left\{{}\begin{matrix}m+1>0\\\Delta=5^2-4\cdot2\left(m+1\right)< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-1\\m>\dfrac{17}{8}\end{matrix}\right.\)
Vậy: \(m>\dfrac{17}{8}\)
2. Cũng chia ra hai trường hợp khi \(m=-1,m\ne-1\) như trên.
Khi \(m\ne-1,f\left(x\right)< 0\forall x\in R\) khi:
\(\left\{{}\begin{matrix}m+1< 0\\\Delta=5^2-4\cdot2\left(m+1\right)< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< -1\\m>\dfrac{17}{8}\end{matrix}\right.\) (vô lí)
Vậy: \(m\in\varnothing\)
3, 4. Làm tương tự như hai ý 1, 2 nhé.
14 tháng 1
TH1: m=-1
\(\Leftrightarrow f\left(x\right)=\left(-1+1\right)x^2+5x+2\)
=>f(x)=5x+2
=>Khi m=-1 thì f(x)>0 khi x>-2/5; f(x)>=0 khi x>=-2/5; f(x)<0 khi x<-2/5; f(x)<=0 khi x<=-2/5
=>Loại
TH2: \(m\ne-1\)
\(f\left(x\right)=\left(m+1\right)x^2+5x+2\)
\(\text{Δ}=5^2-4\cdot\left(m+1\right)\cdot2\)
\(=25-8m-8=-8m+17\)
Để f(x)>=0 với mọi x thì \(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-8m+17< =0\\m+1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-8m< =-17\\m>-1\end{matrix}\right.\Leftrightarrow m>=\dfrac{17}{8}\)
Để f(x)<=0 với mọi x thì \(\left\{{}\begin{matrix}\text{Δ}< =0\\a< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-8m+17< =0\\m+1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>=\dfrac{17}{8}\\m< -1\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
Để f(x)>0 với mọi x thì \(\left\{{}\begin{matrix}\text{Δ}< 0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-8m+17< 0\\m+1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>\dfrac{17}{8}\\m>-1\end{matrix}\right.\Leftrightarrow m>\dfrac{17}{8}\)
Để f(x)<0 với mọi x thì \(\left\{{}\begin{matrix}\text{Δ}< 0\\a< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-8m+17< 0\\m+1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>\dfrac{17}{8}\\m< -1\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
6 tháng 12 2016
\(x+0=0\)
\(\Rightarrow x=0\)
Mà đề bài cho \(x\ne0\Rightarrow x\in\left\{\varphi\right\}\)
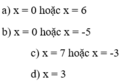
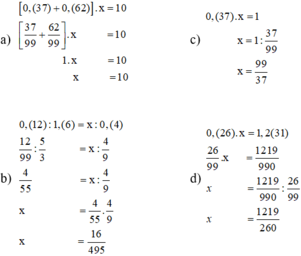
x thuộc tập hợp số hữu tỉ
ko bt có đúng ko ta