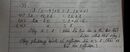x^3+x^2-4x=4 tìm x. thks mn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 4 2019
a) \(x^3-2x^2+x=0\)
\(\Leftrightarrow x\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow x\left(x-1\right)^2=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=1\end{cases}}\)
Vậy....
15 tháng 4 2019
b) \(-x^4-x^2-3=0\)
\(\Leftrightarrow x^4+x^2+3=0\)
\(\Leftrightarrow\left(x^2\right)^2+2\cdot x^2\cdot\frac{1}{2}+\frac{1}{4}+\frac{11}{4}=0\)
\(\Leftrightarrow\left(x^2+\frac{1}{2}\right)^2=\frac{-11}{4}\)( vô lý )
Đa thức vô nghiệm
2 tháng 12 2017
\(A=x^2-4x+1=\left(x^2-2.x.2+4\right)-4+1=\left(x-2\right)^2-3\ge-3\)
\(\Rightarrow MinA=-3\)khi x=2
16 tháng 4 2019
a) Đặt \(A=x^2-2x+5\)
\(=\left(x-1\right)^2+4\)
Ta thấy \(\left(x-1\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-1\right)^2+4\ge0+4\forall x\)
hay \(A\ge4\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow x-1=0\)
\(\Leftrightarrow x=1\)
Vậy Min A=4 \(\Leftrightarrow x=1\)
FF
16 tháng 4 2019
a , \(x^2-2x+5=x^2-2x+1+4=\left(x-1\right)^2+4\ge4\)
Dấu " = " xảy ra khi x - 1 = 0 hay x = 1
Vậy GTNN là 4 khi x = 1 .
b , \(9-4x-x^2=-\left(x^2+4x-9\right)=-\left(x^2+4x+4-13\right)=-\left(x+2\right)^2+13=13-\left(x+2\right)^2\le13\)
Dấu " = " xảy ra khi x + 2 = 0 hay x = -2 .
Vậy GTLN là 13 khi x = -2 .
c , mik ko bt làm
12 tháng 6 2023
2:
=>x^3-1-2x^3-4x^6+4x^6+4x=6
=>-x^3+4x-7=0
=>x=-2,59
4: =>8x-24x^2+2-6x+24x^2-60x-4x+10=-50
=>-62x+12=-50
=>x=1
MY
2
DQ
28 tháng 1 2021
3(x-4)+6=2(x+1)
3x-12+6 =2x+2
3x-2x =2+12-6
x =8
Vậy x=8( nếu là bài tìm x bình thường mà thì ban kết luận như thế)
Vậy phương trình có nghiệm là x=8( Đối vs bài tìm nghiệm)(kết luận ngắn gọn)
Ban đầu mik có chụp ảnh gửi nhg phải chờ phê duyệt nên mik nhắn gửi:3
QT
2
13 tháng 11 2021
\(\Leftrightarrow x^3-ax^2-4=\left(x^2+4x+4\right)\cdot a\left(x\right)=\left(x+2\right)^2\cdot a\left(x\right)\)
Thay \(x=-2\Leftrightarrow-8-4a-4=0\Leftrightarrow a=-3\)
13 tháng 11 2021
\(\Leftrightarrow x^3+4x^2+4x+\left(-4-a\right)x^2-4⋮x^2+4x+4\)
\(\Leftrightarrow-4-a=4+x^2\)
\(\Leftrightarrow a=-4-4-x^2=-x^2-8\)
27 tháng 6 2017
\(A=\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}\)
\(\Leftrightarrow A^2=2x+2\sqrt{x^2-8x+16}=\)
\(=2x+\sqrt{\left(x-4\right)^2}\)
\(=2x+|x-4|\)
\(=\hept{\begin{cases}2x-x+4=x+4\left(2\le x< 4\right)\\2x+x-4=3x-4\left(x\ge4\right)\end{cases}}\)
\(\Rightarrow A=\hept{\begin{cases}\sqrt{x+4}\left(2\le x< 4\right)\\\sqrt{3x-4}\left(x\ge4\right)\end{cases}}\)